minha dúvida é o seguinte estou aprendendo ln e log na faculdade.
a primeira pergunta é :
01-qual tempo de duplicações de preços que estão crescendo a 5% ao ano? eu encontrei isso.
encontrei:
M=c.(1+i)^t
2c=C.(1+i)^t obs: C com C corta
______C
(1+i)^t=2 osb: aqui faz a regra do tombo porque ?
t(1+0,05)=2
t = log2 Obs: por que eu uso o log e não o ln?
___log1,05
resposta: 14,20 anos
e como que eu sei que preciso necessariamente usar o log pra resolver o exercicio inveis do ln? o que eu devo levar em consideração ?
______________________________________________________________________________________________________________
02- A quantidade de A, em mg, que permanece no corpo t horas após ter ingerido um remédio, é dada por A = 10.(0,82)^t
A) quanto tempo leva para permanece no corpo apenas 1 mg do remédio. Resposta: 11,60 horas.
Resolução:
A=10(0,82)^t=1mg
(0,82)^t= 1/10 obs: por que aqui fica 1 sobre 10? por que ta multiplicando e passa dividindo ?
portanto.
ln(0,82)^t=ln(1/10) obs: por que eu faço o ln? o que eu quero encontrar a função inversa?
t=(-0,1984)
_ (-2,3025)
t: 11,60 horas
fico um pouco intenso , mas caso alguém conseguir interpretar o que eu escrevi, vou agradecer muito.




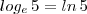 e fazer a mudança de base.
e fazer a mudança de base. .
.
 .
.



