 por SCHOOLGIRL+T » Qua Nov 07, 2012 21:19
por SCHOOLGIRL+T » Qua Nov 07, 2012 21:19
![{32}^{\frac{x+1}{10}}.({\sqrt[5]{16}})^{\frac{5x+5}{8}}= {32}^{\frac{x+1}{10}}.({\sqrt[5]{16}})^{\frac{5x+5}{8}}=](/latexrender/pictures/a20efc7731379cbcd4ccc7e3a1b300da.png)
Para simplificar. Me ajudem?
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Qua Nov 07, 2012 21:24
por Cleyson007 » Qua Nov 07, 2012 21:24
Faça

e

, efetue a multiplicação das potências e encontre o resultado.
Comente qualquer dúvida

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por SCHOOLGIRL+T » Qui Nov 08, 2012 21:15
por SCHOOLGIRL+T » Qui Nov 08, 2012 21:15
Cleyson007 escreveu:Faça

e

, efetue a multiplicação das potências e encontre o resultado.
Comente qualquer dúvida

Não sei se está correto, mas eu consegui resolver e meu resultado deu

. Obrigada!! ^^
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por SCHOOLGIRL+T » Sex Nov 09, 2012 23:44
por SCHOOLGIRL+T » Sex Nov 09, 2012 23:44
Eba! Acertei! Então aprendii! Graças a você! Thanks very much!! =D
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Potenciação e Radiciação
por Carlos22 » Qua Abr 13, 2011 22:06
- 1 Respostas
- 1918 Exibições
- Última mensagem por FilipeCaceres

Qua Abr 13, 2011 22:27
Logaritmos
-
- [Potenciação e Radiciação]
por JU201015 » Seg Nov 12, 2012 22:06
- 2 Respostas
- 1942 Exibições
- Última mensagem por JU201015

Ter Nov 13, 2012 09:08
Álgebra Elementar
-
- Potenciação e radiciação
por anneliesero » Sáb Abr 27, 2013 22:46
- 1 Respostas
- 1654 Exibições
- Última mensagem por e8group

Sáb Abr 27, 2013 23:48
Álgebra Elementar
-
- Potenciação e radiciação
por anneliesero » Sáb Abr 27, 2013 22:51
- 1 Respostas
- 1243 Exibições
- Última mensagem por young_jedi

Dom Abr 28, 2013 21:20
Álgebra Elementar
-
- Potenciação e radiciação
por anneliesero » Sáb Abr 27, 2013 22:53
- 1 Respostas
- 1121 Exibições
- Última mensagem por nakagumahissao

Dom Abr 28, 2013 02:42
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{32}^{\frac{x+1}{10}}.({\sqrt[5]{16}})^{\frac{5x+5}{8}}= {32}^{\frac{x+1}{10}}.({\sqrt[5]{16}})^{\frac{5x+5}{8}}=](/latexrender/pictures/a20efc7731379cbcd4ccc7e3a1b300da.png)

![{32}^{\frac{x+1}{10}}.({\sqrt[5]{16}})^{\frac{5x+5}{8}}= {32}^{\frac{x+1}{10}}.({\sqrt[5]{16}})^{\frac{5x+5}{8}}=](/latexrender/pictures/a20efc7731379cbcd4ccc7e3a1b300da.png)

 e
e  , efetue a multiplicação das potências e encontre o resultado.
, efetue a multiplicação das potências e encontre o resultado.

e
, efetue a multiplicação das potências e encontre o resultado.
 . Obrigada!! ^^
. Obrigada!! ^^

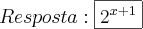


 .
.



