 . Em seguida calcule c para que a solução y satisfaça a condição extra apresentada, para
. Em seguida calcule c para que a solução y satisfaça a condição extra apresentada, para 
Por favor, explique-me de uma maneira simples de se entender. Tenho prova de equações diferenciais esse período, e estou perdido na matéria.

 . Em seguida calcule c para que a solução y satisfaça a condição extra apresentada, para
. Em seguida calcule c para que a solução y satisfaça a condição extra apresentada, para 

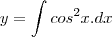

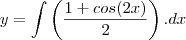
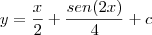






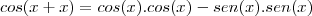
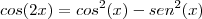
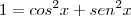






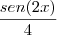 ?
?

young_jedi escreveu:o sen(2x)/4 surgiu do processo de integração

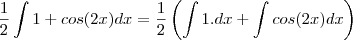


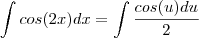
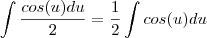
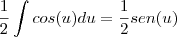
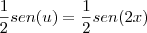

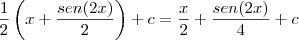

 . Agora pela regra da cadeia
. Agora pela regra da cadeia  . Como no caso temos
. Como no caso temos  , então
, então  .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: