 por Cleyson007 » Qua Nov 07, 2012 21:09
por Cleyson007 » Qua Nov 07, 2012 21:09
Calcule

. Em seguida calcule c para que a solução y satisfaça a condição extra apresentada, para

Por favor, explique-me de uma maneira simples de se entender. Tenho prova de equações diferenciais esse período, e estou perdido na matéria.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por young_jedi » Qui Nov 08, 2012 12:40
por young_jedi » Qui Nov 08, 2012 12:40
substituindo f(x)
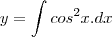
utilizando a relação trigonometrica

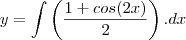
integrando
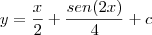
como



portanto c=0
então a resolução da equação fica

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Cleyson007 » Qui Nov 08, 2012 15:46
por Cleyson007 » Qui Nov 08, 2012 15:46
Young_jedi, pode desenvolver essa parte para mim cos² x = 1 + cos 2x / 2 ?
Agradeço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por young_jedi » Qui Nov 08, 2012 15:57
por young_jedi » Qui Nov 08, 2012 15:57
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Cleyson007 » Qui Nov 08, 2012 16:16
por Cleyson007 » Qui Nov 08, 2012 16:16
O processo algébrico não é difícil..
Sabe o que acontece? Estou me perdendo é na "manipulação" da artimanha. Nem me passou pela cabeça que teria de começar por aqui cos(x + x).
Dúvida aqui:

Poderia ser assim?

Outra dúvida: Como surgiu o
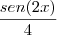
?
Agradeço,
Cleyson007
Editado pela última vez por
Cleyson007 em Qui Nov 08, 2012 16:20, em um total de 1 vez.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por young_jedi » Qui Nov 08, 2012 16:19
por young_jedi » Qui Nov 08, 2012 16:19
Sim, pode ser assim
colocar as constantes para fora da integral facilita bastante
o sen(2x)/4 surgiu do processo de integração
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Cleyson007 » Qui Nov 08, 2012 16:36
por Cleyson007 » Qui Nov 08, 2012 16:36
young_jedi escreveu:o sen(2x)/4 surgiu do processo de integração
Pode me explicar também o procedimento para se chegar em sen (2x) / 4 ?
Agradeço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por young_jedi » Qui Nov 08, 2012 16:50
por young_jedi » Qui Nov 08, 2012 16:50
primeiro eu separei em duas integrais
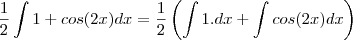
eu fiz integração por substituição
a primeira integral é igual a x
para a segunda eu fiz esta substituição


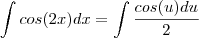
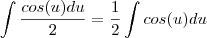
a intgral de cos(u) é sen(u) (como agente bem sabe de derivda)
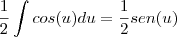
substituindo de volta o x
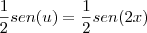
agora voltando a integral principal

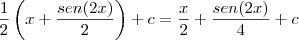
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MarceloFantini » Qui Nov 08, 2012 17:05
por MarceloFantini » Qui Nov 08, 2012 17:05
Pela regra da cadeia, lembre-se que

. Agora pela regra da cadeia

. Como no caso temos

, então

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Diferencial.
por Higor » Seg Fev 21, 2011 13:12
- 4 Respostas
- 12206 Exibições
- Última mensagem por Higor

Seg Fev 21, 2011 14:46
Cálculo: Limites, Derivadas e Integrais
-
- Equaçao diferencial
por romulo39 » Dom Abr 03, 2011 20:58
- 1 Respostas
- 3936 Exibições
- Última mensagem por LuizAquino

Seg Abr 04, 2011 14:39
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial
por jacquelline » Qui Mai 17, 2012 11:04
- 2 Respostas
- 2069 Exibições
- Última mensagem por jacquelline

Sáb Mai 19, 2012 20:37
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 2
por Cleyson007 » Qua Nov 07, 2012 21:14
- 1 Respostas
- 1482 Exibições
- Última mensagem por e8group

Qua Nov 14, 2012 10:06
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 3
por Cleyson007 » Qua Nov 07, 2012 21:19
- 1 Respostas
- 1365 Exibições
- Última mensagem por young_jedi

Qui Nov 08, 2012 12:33
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Em seguida calcule c para que a solução y satisfaça a condição extra apresentada, para
. Em seguida calcule c para que a solução y satisfaça a condição extra apresentada, para 

 . Em seguida calcule c para que a solução y satisfaça a condição extra apresentada, para
. Em seguida calcule c para que a solução y satisfaça a condição extra apresentada, para 

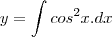

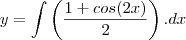
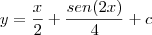






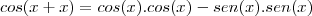
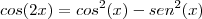
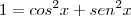






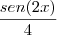 ?
?


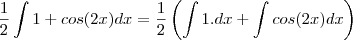


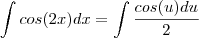
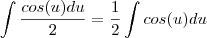
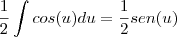
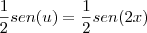

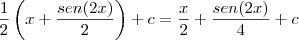

 . Agora pela regra da cadeia
. Agora pela regra da cadeia  . Como no caso temos
. Como no caso temos  , então
, então  .
.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.