![\int_{0}^{2\pi}\sqrt[]{1+cos(x)}dx \int_{0}^{2\pi}\sqrt[]{1+cos(x)}dx](/latexrender/pictures/dfcb67eccacb78184d13813bf60fc60f.png)



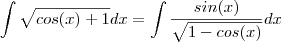
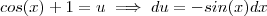 .Assim, segue que :
.Assim, segue que : 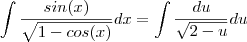
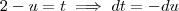

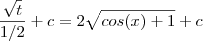
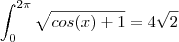

![\int_{}^{}\sqrt[]{cos(x) +1}dx=\int_{}^{}\frac{sin(x)}{\sqrt[]{1-cos(x)}}dx \int_{}^{}\sqrt[]{cos(x) +1}dx=\int_{}^{}\frac{sin(x)}{\sqrt[]{1-cos(x)}}dx](/latexrender/pictures/00d373775e0b3fd7b6826a6bfa36010d.png)

 .
. 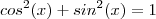 .
. 

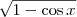 no numerador e denominador, você terá
no numerador e denominador, você terá  sobre
sobre 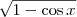 . Ora, mas pela relação fundamental temos
. Ora, mas pela relação fundamental temos 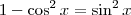 , daí
, daí  . Ou seja, agora você precisa quebrar a integral nos intervalos
. Ou seja, agora você precisa quebrar a integral nos intervalos ![[0, \pi] [0, \pi]](/latexrender/pictures/f74f8710fd31ce502365bc814a7fd3b6.png) e
e ![[\pi, 2 \pi] [\pi, 2 \pi]](/latexrender/pictures/361b499ec6c385d9f8d8f279e29a208f.png) .
.

![sin(x) \geq 0 ; x \in [ 0 , \pi ] sin(x) \geq 0 ; x \in [ 0 , \pi ]](/latexrender/pictures/f3d4b46bcafcaf09f1d6c9a7dec5affc.png)
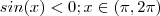 .
.  e
e ![| sin(x) | = sin(x) , x \in [ 0 , \pi ] | sin(x) | = sin(x) , x \in [ 0 , \pi ]](/latexrender/pictures/10b0001ce1f830447ed1727e5c079f63.png) .
.  .
. 
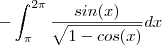
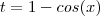 .Donde ,
.Donde ,  . Teremos por um lado ,
. Teremos por um lado ,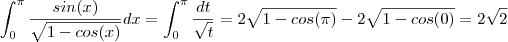 . Entretanto , por outro lado ,
. Entretanto , por outro lado , 
 .
. 
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes

 .
.
 :
: