Olá, boa noite,
Boa noite,
Estava vendo a resolução do colega
Cleyson007 no outro post e como remanesce a sua dúvida, gostaria de discutir alguns pontos com você. Tomei a liberdade de fragmentar a resposta dele aqui pra gente analisar. Fique à vontade para comentar os pontos que você tiver dúvida, vamos lá:
p(x) = a.(x² ? 4) ---> Resolvendo, temos: x' =2 e x'' = -2 ( para qualquer "a")
Nesse passo ele calculou as raízes do
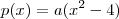
Perceba que "a" deve ser diferente de zero, caso contrário p(x) será um ponto.
O que está sendo dito é que não podemos ter

, caso contrário não teremos uma curva para cortar o gráfico dado no problema.
Como pelo enunciado a<0 ,trata-se de uma parábola com concavidade para baixo, cortando eixo "x" nas raizes, sendo portanto dois pontos fixos que cortam o grafico f(x). Agora cabe a nós calcularmos os outros dois pontos.
Aqui você há de se lembrar que quando o coeficiente de

é negativo numa função quadrática então sua concavidade é para baixo.
Perceba que o vértice da parábola encontra-se sobre o eixo "y" e que yv deve estar entre 0 e 2 para que os braços da parabola "cortem" os dois segmentos de reta caracterizando os dois pontos faltantes.
Em outras palavras, se o y do vértice dessa parábola for maior do que ou igual a 2, então a parte de cima da parábola não cortará o gráfico da função do problema em outros dois pontos para completar os quatro pedidos ( os primeiros dois são as raízes que já foram calculadas ).
yv = -delta / 4a ==>> (-16a²) / 4a = -4a
Aqui você há de se lembrar que o y do vértice da parábola é dado por
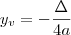
.
0 < yv < 2 -->> 0 < - 4a < 2
Aqui está sendo usado o fato de que, para atender ao problema, o y do vértice não pode ser maior do que 2. Também não pode ser menor do que ou igual a zero pela condição de

.
0 < - 4a --->> 0 > a (I)
-4a < 2--->> a > -1/2 (II)
Aqui fez-se as contas e concluiu que
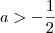
, o mesmo que
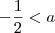
Observando as duas condições obtemos como resposta: -1/2 < a <0
Do resultado anterior e do fato de que

conluiu-se que
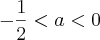
.
.



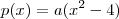
 , caso contrário não teremos uma curva para cortar o gráfico dado no problema.
, caso contrário não teremos uma curva para cortar o gráfico dado no problema. é negativo numa função quadrática então sua concavidade é para baixo.
é negativo numa função quadrática então sua concavidade é para baixo. .
.  .
.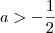 , o mesmo que
, o mesmo que 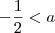
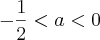 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
