 por Ronaldobb » Ter Nov 06, 2012 21:43
por Ronaldobb » Ter Nov 06, 2012 21:43
-
Ronaldobb
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Ter Set 18, 2012 19:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por Ronaldobb » Ter Nov 06, 2012 21:45
por Ronaldobb » Ter Nov 06, 2012 21:45
A letra (d) está com erro:
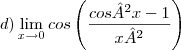
-
Ronaldobb
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Ter Set 18, 2012 19:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por MarceloFantini » Ter Nov 06, 2012 23:41
por MarceloFantini » Ter Nov 06, 2012 23:41
Suponho que talvez eles possam ser resolvidos por L'Hospital, mas não que seja necessário. Além disso, crie um novo tópico para cada dúvida. Em outras palavras, crie um tópico para cada limite. Escolha um e deixe aqui, mas os outros crie novos tópicos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Regra de l'Hopital
por Claudin » Seg Mai 16, 2011 16:05
- 15 Respostas
- 10939 Exibições
- Última mensagem por deangelo

Sex Jun 10, 2011 15:23
Cálculo: Limites, Derivadas e Integrais
-
- Regra de l'Hôpital.
por matematicouff » Qui Jun 21, 2012 17:12
- 1 Respostas
- 1490 Exibições
- Última mensagem por Russman

Qui Jun 21, 2012 17:22
Cálculo: Limites, Derivadas e Integrais
-
- [Dúvida] Regra de L'hôpital
por Borracha22 » Ter Mai 28, 2013 18:38
- 2 Respostas
- 3710 Exibições
- Última mensagem por Man Utd

Ter Mai 28, 2013 23:11
Cálculo: Limites, Derivadas e Integrais
-
- [Regra de L'Hôpital]me ajudem nesse exercício.
por marcosmuscul » Sáb Abr 13, 2013 14:07
- 1 Respostas
- 1509 Exibições
- Última mensagem por e8group

Sáb Abr 13, 2013 14:41
Cálculo: Limites, Derivadas e Integrais
-
- [Ajuda] Regra de Simpson
por kaaps » Sáb Mai 12, 2012 20:54
- 1 Respostas
- 1906 Exibições
- Última mensagem por LuizAquino

Seg Mai 14, 2012 09:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




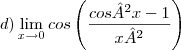


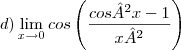



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.