Ok, vamos por partes...
Sabemos que quando uma função

possui uma base definida e com a variável

restrita no conjunto dos números Naturais, ela é uma PG, exemplo:
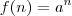
.
Sabemos também que quando uma função

não tem base definida e a viarável

está restrita no cojunto dos números Naturias, ela é uma PA, exemplo:
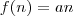
.
Então, na minha ótica, assim como existe Somatório e Produtório, Média Aritmética e Geométrica,
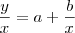
e
![\sqrt[x]{y}=a\cdot \sqrt[x]{b} \sqrt[x]{y}=a\cdot \sqrt[x]{b}](/latexrender/pictures/4159994b867d4af09e0d60fb9fc6c1d8.png)
,
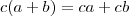
e
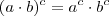
, deve existir também uma paralela para a tx de variação
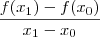
, no caso:
![\sqrt[\frac{x_1}{x_0}]{\frac{f(x_1)}{f(x_0)}} \sqrt[\frac{x_1}{x_0}]{\frac{f(x_1)}{f(x_0)}}](/latexrender/pictures/f62910bdfff2304664d7fa47ccb825ab.png)
Ou seja, na minha ótica, a álgebra matemática ou é da classe aritmética ou é da classe geométrica. Ok, e o que isso tem haver com existir ou não uma base neutra?
Simples, se existir uma base neutra, então toda função polinomial, que é da classe aritmética, pode ser expressa com uma base de definida (no caso: a neutra) e, portanto, se possui base, é da classe geométrica. Mas como não existe tal base, então não é possível expressar uma função linear com uma base que não altere a linearidade, ou seja, toda função polinomial é estritamente aritmética.
Agora, uma função exponencial do tipo
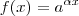
, além de possui uma base

definida, que a classifica, no meu ponto de vista, como uma função do tipo geométrica, também possui um expoente

que é coeficente de da variável

.

é o que eu chamo de tx de variação geométrica, e essa tx eu descubro aplicando o limite que postei acima, ademais,

no contexto duma PG, se relaciona com a razão entre termos consecutivos, já o

é a tx de variação aritmética, como eu sei disso? Sei pq o Elon Lages Lima disse que é e pq eu já vi como esse coeficente

de comporta numa escala logaritmica, além disso, esse coeficente também se relaciona com a diferença entre termos consecutivos duma PA. Portanto, uma função exponencial possui duas taxas de variação, a aritmética e a geométrica, logo, toda PG também é uma PA.
O Limite que postei acima, descobri quando procurava uma forma de chegar sistematicamente numa PG de 2ª ordem. Eu percebi que o cálculo diferencial e integral cai como uma luva para alterar a ordem duma função que não possui base definida, ou seja, somente para funções do tipo do aritmética. Mas, como eu disse, o que eu queria era uma função cuja tx de variação é

e a primitiva, neste caso, é:
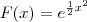
. Daí a necessidade de destinguir o conceito de taxa de variação aritmética e geométrica.
Se tudo é para os Reais ou para os Complexos eu não sei. Tudo o que fiz foi baseado no gosto de fazer, pensar e raciocinar sobre conceitos algébricos, e, depois, chegar a conclusões abrangentes e gerais. Sobre estudar, ultimamente não estou sendo muito fã disso, pq os livros sempre demonstram o assunto de forma fragmentada. Eu, por exemplo, estou analisando o conceito de proporcionalidade e já cheguei 4 equações fundamentais que delas decorrem 8 funções distintas, nenhum livro sobre proporção trata de todos os possiveis caso, estou analisando a possibilidade de grandezas proporcionais de 2ª ordem, teorema de tales para curvas, etc... e assim vou levando...
 qualquer, é razoável pensarmos que
qualquer, é razoável pensarmos que  está sendo somado e subtraído por zero, multiplicado e dividido por 1 e elevado e extraído a raiz de 1, ok! Estes são os tais elementos neutros. Mas porque não conseguimos definir uma base neutra para
está sendo somado e subtraído por zero, multiplicado e dividido por 1 e elevado e extraído a raiz de 1, ok! Estes são os tais elementos neutros. Mas porque não conseguimos definir uma base neutra para  ?
?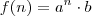 (proveniente de:
(proveniente de: 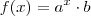 ), a sua PG de 2ª ordem é
), a sua PG de 2ª ordem é 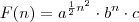
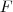 é esta mesmo.
é esta mesmo.![\lim_{h->0} \sqrt[h]{\frac{f(x+h)}{f(x)}} \lim_{h->0} \sqrt[h]{\frac{f(x+h)}{f(x)}}](/latexrender/pictures/773323a5adaddee9b66b2f8819194e95.png)
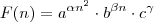
 , então:
, então: 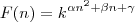
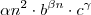 é uma PA de 2ª ordem!
é uma PA de 2ª ordem! e
e  , enquanto que
, enquanto que  é o valior inicial. A tx de variação geométrica, que é a razão entre termos consecutivos, está relacionada com as bases e seus respectivos expoentes (novamente, basta aplicar o limite acima para confirmar isso), que é
é o valior inicial. A tx de variação geométrica, que é a razão entre termos consecutivos, está relacionada com as bases e seus respectivos expoentes (novamente, basta aplicar o limite acima para confirmar isso), que é  e
e 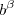 , enquanto que
, enquanto que 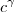 é o valor inicial.
é o valor inicial.


 possui uma base definida e com a variável
possui uma base definida e com a variável 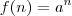 .
.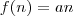 .
.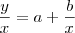 e
e ![\sqrt[x]{y}=a\cdot \sqrt[x]{b} \sqrt[x]{y}=a\cdot \sqrt[x]{b}](/latexrender/pictures/4159994b867d4af09e0d60fb9fc6c1d8.png) ,
, 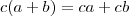 e
e 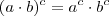 , deve existir também uma paralela para a tx de variação
, deve existir também uma paralela para a tx de variação 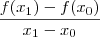 , no caso:
, no caso: ![\sqrt[\frac{x_1}{x_0}]{\frac{f(x_1)}{f(x_0)}} \sqrt[\frac{x_1}{x_0}]{\frac{f(x_1)}{f(x_0)}}](/latexrender/pictures/f62910bdfff2304664d7fa47ccb825ab.png)
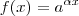 , além de possui uma base
, além de possui uma base  definida, que a classifica, no meu ponto de vista, como uma função do tipo geométrica, também possui um expoente
definida, que a classifica, no meu ponto de vista, como uma função do tipo geométrica, também possui um expoente  e a primitiva, neste caso, é:
e a primitiva, neste caso, é: 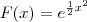 . Daí a necessidade de destinguir o conceito de taxa de variação aritmética e geométrica.
. Daí a necessidade de destinguir o conceito de taxa de variação aritmética e geométrica.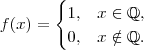


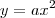 ser ou ñ ser uma equação do tipo diretamente proporcional e o por que, questão de nível fundamental. Já neste tópico, eu tento relacionar o coneito de tx de variação com as razões das PG e com as diferenças das PA. Eu dúvido que uma faculdade de matemática ensina tudo por a+b, dúvido! A matemática do ensino fundamental e médio é tão simples e tão mal ensinda, imagino então como é a de ensino superior, que é cheio de detalhes. Enfim, creio que cursar uma faculdade de matemática, além de aumentar meus conhecimentos, irá aumentar proporcionalmente as minhas dúvidas e lacunas.
ser ou ñ ser uma equação do tipo diretamente proporcional e o por que, questão de nível fundamental. Já neste tópico, eu tento relacionar o coneito de tx de variação com as razões das PG e com as diferenças das PA. Eu dúvido que uma faculdade de matemática ensina tudo por a+b, dúvido! A matemática do ensino fundamental e médio é tão simples e tão mal ensinda, imagino então como é a de ensino superior, que é cheio de detalhes. Enfim, creio que cursar uma faculdade de matemática, além de aumentar meus conhecimentos, irá aumentar proporcionalmente as minhas dúvidas e lacunas.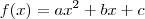
 . Ora, se existe equações quadráticas, então também existe equações cúbicas, lineares? Sim, [...].
. Ora, se existe equações quadráticas, então também existe equações cúbicas, lineares? Sim, [...].