 por fabriel » Seg Nov 05, 2012 13:49
por fabriel » Seg Nov 05, 2012 13:49
E ai galera blz. então é dado o exercício ai:
#Considere a função f:R-R definida por

para cada xeR. A área da região limitada pelo gráfico
da função y=f(x), o eixo Ox e as retas x=0 e x=2
é igual a.
Resolvendo a integral:

Vamos obter:
![\left[\frac{{x}^{5}}{5}-\frac{{5x}^{3}}{3}+4x \right] \left[\frac{{x}^{5}}{5}-\frac{{5x}^{3}}{3}+4x \right]](/latexrender/pictures/cf402c6dc19567ada24f1f061d1cd33e.png)
Avaliado nos pontos 0 e 2. obtemos então:

Mas pelo que vi no gabarito a resposta certa é:
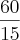
E não entendi o que eu errei..Poderiam me ajudar nessa questão.
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por MarceloFantini » Seg Nov 05, 2012 15:22
por MarceloFantini » Seg Nov 05, 2012 15:22
A curva tem uma raíz em

e passa a ser negativa. Normalmente quando integramos esta área é considerada "negativa" pelo fato de estar orientada "negativamente". Para obter o valor absoluto da área sob a curva, integre de 0 a 1 normalmente e depois tome o módulo da integral de 1 a 2. O resultado será como está no gabarito.
Veja
aqui o que eu quero dizer.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fabriel » Seg Nov 05, 2012 16:57
por fabriel » Seg Nov 05, 2012 16:57
Entendi, muito obrigado!!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Exercício de integral definida]
por Reis » Qui Jun 09, 2016 19:33
- 1 Respostas
- 4073 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 11, 2016 09:15
Cálculo: Limites, Derivadas e Integrais
-
- [integral definida] - dúvida em exercício
 por natanaelskt » Qua Jul 02, 2014 02:13
por natanaelskt » Qua Jul 02, 2014 02:13
- 1 Respostas
- 1914 Exibições
- Última mensagem por e8group

Qua Jul 02, 2014 14:04
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4346 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Função definida por ramos]Exercício
por fff » Qua Jan 22, 2014 10:51
- 0 Respostas
- 1728 Exibições
- Última mensagem por fff

Qua Jan 22, 2014 10:51
Funções
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3681 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\left[\frac{{x}^{5}}{5}-\frac{{5x}^{3}}{3}+4x \right] \left[\frac{{x}^{5}}{5}-\frac{{5x}^{3}}{3}+4x \right]](/latexrender/pictures/cf402c6dc19567ada24f1f061d1cd33e.png) Avaliado nos pontos 0 e 2. obtemos então:
Avaliado nos pontos 0 e 2. obtemos então: 
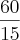


 e passa a ser negativa. Normalmente quando integramos esta área é considerada "negativa" pelo fato de estar orientada "negativamente". Para obter o valor absoluto da área sob a curva, integre de 0 a 1 normalmente e depois tome o módulo da integral de 1 a 2. O resultado será como está no gabarito.
e passa a ser negativa. Normalmente quando integramos esta área é considerada "negativa" pelo fato de estar orientada "negativamente". Para obter o valor absoluto da área sob a curva, integre de 0 a 1 normalmente e depois tome o módulo da integral de 1 a 2. O resultado será como está no gabarito.



 , avisa que eu resolvo.
, avisa que eu resolvo.

