Como resolver:
6,25?3=
A resposta é 10,8



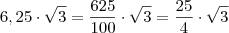 .
.  .
. 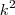 fica bem próximo de 3 [/tex] .
fica bem próximo de 3 [/tex] . e
e 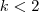 .Pois
.Pois 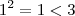 e
e  . Sendo assim podemos dizer que ,
. Sendo assim podemos dizer que , 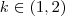 .
.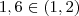 e
e 
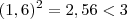 e
e 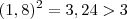
 .
. 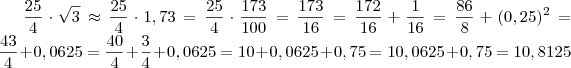 .
. 
Voltar para Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: