 por Jhenrique » Qui Nov 01, 2012 21:39
por Jhenrique » Qui Nov 01, 2012 21:39
Gostaria de saber qual é o 1º, o 2º, o 3º e o 4º quadrante no plano xz e no plano yz.
Obrigado.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Niiseek » Qui Nov 01, 2012 22:34
por Niiseek » Qui Nov 01, 2012 22:34
Não entendi muito bem o que perguntou mas vou tentar te ajudar, me deixou muito confuso.
O quadrante se usa no plano cartesiano (x,y) onde:
1º quadrante: do 0º ao 90º
2º quadrante: do 90º ao 180º
3º quadrante: do 180º ao 270º
4º quadrante: 270º ao 360º
Te explicando melhor:
tendo X>0 e Y>0 você está no 1º quadrante.
tendo X<0 e Y>0 você está no 2º quadrante.
tendo X<0 e Y<0 você está no 3º quadrante.
tendo X>0 e Y<0 você está no 4º quadrante.
Se entendi bem você quer saber onde se localizam os quadrantes, ai está suas posições. Agora se for algo mais especifico como você perguntou, plano xz e plano yz não sei se essa resposta serve.
-
Niiseek
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Out 29, 2012 16:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por Jhenrique » Qui Nov 01, 2012 22:40
por Jhenrique » Qui Nov 01, 2012 22:40
Agradeço pelo força! Mas a minha dúvida é realmente com relação aos planos xz e yz!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sex Nov 02, 2012 07:36
por MarceloFantini » Sex Nov 02, 2012 07:36
Niiseek escreveu:tendo X>0 e Z>0 você está no 1º quadrante.
tendo X<0 e Z>0 você está no 2º quadrante.
tendo X<0 e Z<0 você está no 3º quadrante.
tendo X>0 e Z<0 você está no 4º quadrante.
Apenas adaptei, analogamente para

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Sex Nov 02, 2012 11:03
por Jhenrique » Sex Nov 02, 2012 11:03
MarceloFantini escreveu:Niiseek escreveu:tendo X>0 e Z>0 você está no 1º quadrante.
tendo X<0 e Z>0 você está no 2º quadrante.
tendo X<0 e Z<0 você está no 3º quadrante.
tendo X>0 e Z<0 você está no 4º quadrante.
Apenas adaptei, analogamente para

.
Na vdd, vc adaptou para
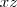
gostaria de saber tbm para

.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sex Nov 02, 2012 11:05
por MarceloFantini » Sex Nov 02, 2012 11:05
Não existe diferença, você sabe trocar letras.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Sex Nov 02, 2012 14:04
por Jhenrique » Sex Nov 02, 2012 14:04
A convenção, então, é como na representação abaixo?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sex Nov 02, 2012 16:17
por MarceloFantini » Sex Nov 02, 2012 16:17
Em geral não perdemos tempo com esses detalhes bobos, mas se existisse uma convenção, acredito que seria esta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Sex Nov 02, 2012 22:28
por Jhenrique » Sex Nov 02, 2012 22:28
Não é uma coisa tão boba assim quando se estuda geometria descritiva e se percebe que é convenção mundial representar um objeto 3D num diedro, e não num triedro, o que eu considero um absurdo, e, como se já não bastasse, sem nem se quer definir os eixos de antemão.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 .
.

.
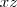 gostaria de saber tbm para
gostaria de saber tbm para  .
.




