 por Danilo » Qua Out 31, 2012 02:36
por Danilo » Qua Out 31, 2012 02:36
Dados os planos

1: x-y+z+1 = 0 e

2 : x+y-z-1=0, determine o plano que contém

1
interseção com

2 e é ortogonal ao vetor (1,1,-1).
Bom, sei que a interseção entre dois planos é uma reta... e como encontrar equação de planos e retas mas não sei como aplicar no exercício. Grato desde já!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Qua Out 31, 2012 07:12
por MarceloFantini » Qua Out 31, 2012 07:12
Encontre a reta que é interseção de
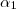
com
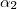
. Uma forma de fazer é encontrar um vetor
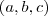
tal que o produto vetorial dele com o vetor diretor da reta seja

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Danilo » Sex Nov 02, 2012 02:38
por Danilo » Sex Nov 02, 2012 02:38
MarceloFantini escreveu:Encontre a reta que é interseção de
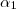
com
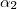
. Uma forma de fazer é encontrar um vetor
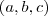
tal que o produto vetorial dele com o vetor diretor da reta seja

.
Bom, a primeira coisa que fiz foi fazer o produto vetorial das normais dos planos dados. Para mim, a normal encontrada será o vetor diretor da reta que quero encontrar (corrijam-me se eu estiver errado.). Aí depois eu encontrei o ponto (0,1,0) que é a solução do sistema dos planos dados... e encontrei uma equação (que nao corresponde a resposta correta...). Onde estou errando?
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Sex Nov 02, 2012 08:23
por MarceloFantini » Sex Nov 02, 2012 08:23
Danilo escreveu:Bom, a primeira coisa que fiz foi fazer o produto vetorial das normais dos planos dados. Para mim, a normal encontrada será o vetor diretor da reta que quero encontrar (corrijam-me se eu estiver errado.). Aí depois eu encontrei o ponto (0,1,0) que é a solução do sistema dos planos dados... e encontrei uma equação (que nao corresponde a resposta correta...). Onde estou errando?
O produto vetorial realmente é o vetor diretor da reta que você quer encontrar, mas você quer encontrar
um plano. A outra condição que este plano deve satisfazer é ser ortogonal a

, logo tome um vetor que seja ortogonal a ele, como
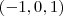
.
Todas as condições foram satisfeitas agora. A equação será
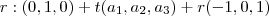
, onde
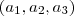
é o vetor que você encontrou no produto vetorial.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação vetorial da reta/plano
por Danilo » Dom Nov 04, 2012 13:23
- 2 Respostas
- 4883 Exibições
- Última mensagem por Danilo

Dom Nov 04, 2012 16:51
Geometria Analítica
-
- Equação vetorial da reta/plano
por Danilo » Ter Nov 06, 2012 14:58
- 5 Respostas
- 5691 Exibições
- Última mensagem por Danilo

Ter Nov 06, 2012 20:09
Geometria Analítica
-
- Encontrar equação (vetorial) da reta
por elisafrombrazil » Qua Abr 19, 2017 21:52
- 0 Respostas
- 1820 Exibições
- Última mensagem por elisafrombrazil

Qua Abr 19, 2017 21:52
Álgebra Linear
-
- [RETAS] equação vetorial de reta que corta outras duas
por renan_a » Seg Out 01, 2012 19:32
- 3 Respostas
- 2030 Exibições
- Última mensagem por young_jedi

Seg Out 01, 2012 22:04
Geometria Analítica
-
- [Cálculo Vetorial - Parametrização] - Reta
por anselmojr97 » Dom Mar 20, 2016 01:25
- 0 Respostas
- 2514 Exibições
- Última mensagem por anselmojr97

Dom Mar 20, 2016 01:25
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 1: x-y+z+1 = 0 e
1: x-y+z+1 = 0 e  2 : x+y-z-1=0, determine o plano que contém
2 : x+y-z-1=0, determine o plano que contém  1
1 2 e é ortogonal ao vetor (1,1,-1).
2 e é ortogonal ao vetor (1,1,-1).

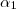 com
com 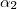 . Uma forma de fazer é encontrar um vetor
. Uma forma de fazer é encontrar um vetor 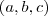 tal que o produto vetorial dele com o vetor diretor da reta seja
tal que o produto vetorial dele com o vetor diretor da reta seja  .
.

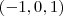 .
.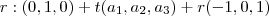 , onde
, onde 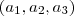 é o vetor que você encontrou no produto vetorial.
é o vetor que você encontrou no produto vetorial.
 .
.



