Sub-seção para materiais das disciplinas relacionadas ao Instituto de Física.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por Cleyson007 » Seg Out 29, 2012 19:33
por Cleyson007 » Seg Out 29, 2012 19:33
Faça uso de integração para resolver o exercício!
Sueli está dirigindo um carro em um trecho retilíneo de uma estrada. No tempo t = 0, quando está se movendo a 10m/s no sentido positivo do eixo Ox, ela passa por um poste de sinalização a uma distância x = 50m. Sua aceleração em função do tempo é dada por: ax = 2,0m/s² - (0,10m/s³)t.
a) Deduza uma expressão para a posição e a velocidade em função do tempo.
b) Qual é o instante em que sua velocidade atinge o valor máximo?
c) Qual é a velocidade máxima?
d) Onde está o carro quando a velocidade atinge seu valor máximo?
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Russman » Seg Out 29, 2012 20:37
por Russman » Seg Out 29, 2012 20:37
Se
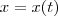
é a função que descreve o movimento da partícula então sua velocidade , também em função do tempo , que é a taxa com que esta varia de posição,
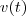
e dada por
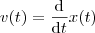
. Ainda, a sua aceleração, que é a taxa com que a velocidade varia no tempo, é dada por
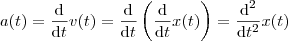
.
Assim, observe que:


Portanto, para calcular as funções de posição e velocidade basta integrar a função aceleração.
Sabemos que uma função real de uma variável atinge o seu ponto extremo ( máximo ou mínimo) quando sua derivada com relação a esta variável é nula. Portanto calcule a função velocidade, derive e iguale a zero. Veja que isto é equivalente a calcular o instante em que a aceleração se anula.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Cleyson007 » Seg Out 29, 2012 21:14
por Cleyson007 » Seg Out 29, 2012 21:14
Boa noite Russman,
Primeiramente, muito obrigado pela EXCELENTE explicação!!
Por favor veja se estou correto:
a)

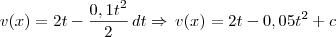

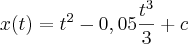
b)

--> Essa constante "c" não vai atrapalhar quando aplicar Bháskara?
No aguardo,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Russman » Seg Out 29, 2012 21:25
por Russman » Seg Out 29, 2012 21:25
Ok, você encontrou
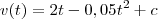
.
Observe que tomando

temos

. O exercício diz que nesses instante o móvel estava se movendo a 10 m/s. Assim,
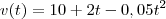
.
Agora para calcular

integre
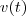
:

Faça o mesmo procedimento que fiz para calcular a constante

.
Na letra b) você precisa calcular para qual tempo

que a velocidade atinge seu valor máximo. Como eu disse, uma função real de uma variável atinge o seu ponto extremo ( máximo ou mínimo) quando sua derivada com relação a esta variável é nula.
Portanto, fazendo

temos
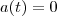
. Como
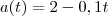
, então

.
No instante

segundos o móvel atinge sua máxima velocidade. Esta você calcula fazendo

em
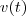
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Cleyson007 » Seg Out 29, 2012 21:48
por Cleyson007 » Seg Out 29, 2012 21:48
Russman, quando temos t = 0 temos x (t = 0) = 10t + t² - 0,017t³ + c --> c = 50
10t + t² - 0,017t³ + 50 = x(t)
Como você disse, a velocidade máxima é atingida em t = 20s.
v(t) = 2(20) - 0,05 (20)² + 10 --> v(t) = 10 + 40 - 20 --> v(t) = 30m/s
É isso?
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Russman » Seg Out 29, 2012 21:52
por Russman » Seg Out 29, 2012 21:52
Isto mesmo! (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Cleyson007 » Ter Out 30, 2012 10:31
por Cleyson007 » Ter Out 30, 2012 10:31
Ok Russman!
Como resolvo a letra "d"?
Sai por aqui
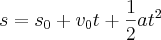
, ou por aqui

?
No aguardo,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Física
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integração por Partes] Constante de integração
por KleinIll » Dom Set 01, 2019 14:11
- 2 Respostas
- 5941 Exibições
- Última mensagem por KleinIll

Sex Set 06, 2019 18:39
Cálculo: Limites, Derivadas e Integrais
-
- [Limites de Integração] Como achar os limites de integração?
por Miine_J » Sáb Nov 10, 2018 03:13
- 2 Respostas
- 19668 Exibições
- Última mensagem por Miine_J

Dom Nov 11, 2018 08:17
Cálculo: Limites, Derivadas e Integrais
-
- Integração
por dexter » Ter Fev 05, 2013 11:14
- 3 Respostas
- 1461 Exibições
- Última mensagem por e8group

Ter Fev 05, 2013 19:45
Cálculo: Limites, Derivadas e Integrais
-
- INTEGRAÇÃO POR PARTES
por clarivando » Sex Fev 06, 2009 12:03
- 3 Respostas
- 7385 Exibições
- Última mensagem por Marcampucio

Seg Mar 16, 2009 15:50
Cálculo: Limites, Derivadas e Integrais
-
- Integração por partes
por clarivando » Sáb Fev 07, 2009 19:10
- 1 Respostas
- 1986 Exibições
- Última mensagem por clarivando

Ter Fev 10, 2009 20:26
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



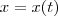 é a função que descreve o movimento da partícula então sua velocidade , também em função do tempo , que é a taxa com que esta varia de posição,
é a função que descreve o movimento da partícula então sua velocidade , também em função do tempo , que é a taxa com que esta varia de posição, 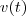 e dada por
e dada por 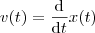 . Ainda, a sua aceleração, que é a taxa com que a velocidade varia no tempo, é dada por
. Ainda, a sua aceleração, que é a taxa com que a velocidade varia no tempo, é dada por 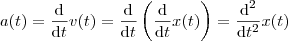 .
.


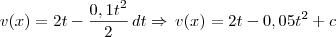

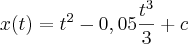
 --> Essa constante "c" não vai atrapalhar quando aplicar Bháskara?
--> Essa constante "c" não vai atrapalhar quando aplicar Bháskara?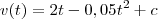 .
. temos
temos  . O exercício diz que nesses instante o móvel estava se movendo a 10 m/s. Assim,
. O exercício diz que nesses instante o móvel estava se movendo a 10 m/s. Assim, 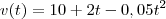 .
. integre
integre 
 .
. que a velocidade atinge seu valor máximo. Como eu disse, uma função real de uma variável atinge o seu ponto extremo ( máximo ou mínimo) quando sua derivada com relação a esta variável é nula.
que a velocidade atinge seu valor máximo. Como eu disse, uma função real de uma variável atinge o seu ponto extremo ( máximo ou mínimo) quando sua derivada com relação a esta variável é nula. temos
temos 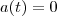 . Como
. Como 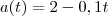 , então
, então  .
. segundos o móvel atinge sua máxima velocidade. Esta você calcula fazendo
segundos o móvel atinge sua máxima velocidade. Esta você calcula fazendo 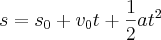 , ou por aqui
, ou por aqui  ?
?![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)