 por brunosob » Dom Out 28, 2012 12:51
por brunosob » Dom Out 28, 2012 12:51
Dadas a reta: 6x - 6y + 1 = 0
Calcular a distância da reta perpendicular a esta reta e que passa pelo (-1,-1), até a origem do sistema cartesiano.
Olá pessoal, estou com dúvida tanto na resolução quanto na interpretação da questão acima,
Por gentileza, preciso de uma resolução detalhada para o entendimento da questão. Aguardo, Grato
-
brunosob
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Out 28, 2012 12:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Contábeis
- Andamento: cursando
 por MarceloFantini » Dom Out 28, 2012 14:56
por MarceloFantini » Dom Out 28, 2012 14:56
Você tem uma reta inclinada. Existem infinitas retas perpendiculares a ela. Uma delas com certeza passa pelo ponto dado

. Agora trace um segmento da origem até esta reta, perpendicular. Esta é a distância que você quer.
Para resolver, encontre o coeficiente angular da reta perpendicular, substitua na equação
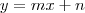
juntamente com o ponto

para encontrar o coeficiente linear. Daí tente calcular a distância.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DERIVADA] Reta tangente e Reta perpendicular
por antonelli2006 » Ter Nov 22, 2011 11:21
- 1 Respostas
- 8666 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 14:28
Cálculo: Limites, Derivadas e Integrais
-
- [Reta perpendicular]
por temujin » Qua Mai 29, 2013 19:35
- 2 Respostas
- 1630 Exibições
- Última mensagem por temujin

Seg Jul 15, 2013 20:04
Geometria Analítica
-
- [Cálculo de distancia] Calcular a distancia de um ponto (B)
por girli » Dom Mai 18, 2014 17:59
- 1 Respostas
- 3882 Exibições
- Última mensagem por jcmatematica

Sex Set 26, 2014 10:43
Geometria Plana
-
- [Eq. Geral do plano] perpendicular a uma reta
por ilariun » Qua Nov 23, 2011 10:45
- 1 Respostas
- 1808 Exibições
- Última mensagem por LuizAquino

Qua Nov 23, 2011 21:02
Geometria Analítica
-
- Seja ? um plano e b uma reta não perpendicular
por GILSON DOS SANTOS » Qui Ago 23, 2012 14:16
- 1 Respostas
- 1409 Exibições
- Última mensagem por MarceloFantini

Qui Ago 23, 2012 16:18
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 . Agora trace um segmento da origem até esta reta, perpendicular. Esta é a distância que você quer.
. Agora trace um segmento da origem até esta reta, perpendicular. Esta é a distância que você quer.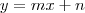 juntamente com o ponto
juntamente com o ponto 

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.