Encontrar a equação do plano que passa pelos pontos P = (1,0,0) e Q = (1,0,1) e é perpendicular ao plano y = z.
Bom, eu sei que para encontrar a equação do plano basta encontrar a sua normal (já que eu já tenho pontos dados pertencentes a ele). E eu sei que a normal do plano y=z (plano esse que eu não consigo enxergar) é perpendicular ao plano que quero encontrar. Mas eu não sei como terminar.... !





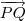 tambem, portanto o produto vetorial dos dois fornece um vetor normal ao plano que voce quer determinar
tambem, portanto o produto vetorial dos dois fornece um vetor normal ao plano que voce quer determinar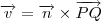
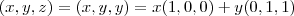 . Você pode encontrar a normal fazendo o produto vetorial dos vetores diretores.
. Você pode encontrar a normal fazendo o produto vetorial dos vetores diretores. já pertence, basta substituir
já pertence, basta substituir  na equação geral e encontrar o coeficiente que falta.
na equação geral e encontrar o coeficiente que falta.


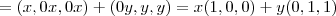 .
. e
e  são números, ou seja, escalares, e portanto se tiver um vetor que todas as coordenadas estejam multiplicadas por eles, podemos colocá-lo para fora.
são números, ou seja, escalares, e portanto se tiver um vetor que todas as coordenadas estejam multiplicadas por eles, podemos colocá-lo para fora.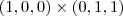 . Eles são os vetores diretores do plano, conforme os argumentos acima.
. Eles são os vetores diretores do plano, conforme os argumentos acima. .
.