 por manuoliveira » Ter Out 23, 2012 20:34
por manuoliveira » Ter Out 23, 2012 20:34
Ache o comprimento do arco da curva definida por x = t³/3 e y = t²/2 do ponto A = (0, 0) ao ponto B = (1/3, 1/2)
Agradeço desde já quem puder ajudar!!!
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por manuoliveira » Ter Out 23, 2012 20:44
por manuoliveira » Ter Out 23, 2012 20:44
Cheguei ao resultado 1/3 mas não tenho gabarito. Gostaria de saber se confere. Caso não, como resolver?
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por young_jedi » Ter Out 23, 2012 20:53
por young_jedi » Ter Out 23, 2012 20:53
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Russman » Ter Out 23, 2012 20:59
por Russman » Ter Out 23, 2012 20:59
Suponhamos que o comprimento da curva entre os pontos

e

seja

. Vamos dividir esse arco em

pequenos intervalos
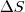
de forma que

.
Quanto menores forem estes intervalos mais exato se torna essa aproximação de forma que

.
Como
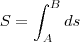
basta tomarmos

e integrar.
Veja que a curva esta parametrizada, isto é,
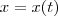
e

de onde
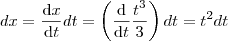
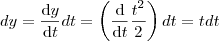
e portanto

.
O ponto

é obtido tomando

e o

tomando

. Finalmente,

.
Agora basta integral. (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por manuoliveira » Ter Out 23, 2012 21:43
por manuoliveira » Ter Out 23, 2012 21:43
Obrigada!!
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- comprimento do arco
por liviabgomes » Seg Mai 30, 2011 16:11
- 10 Respostas
- 6210 Exibições
- Última mensagem por liviabgomes

Qua Jun 01, 2011 15:03
Cálculo: Limites, Derivadas e Integrais
-
- comprimento de arco
por manuoliveira » Ter Out 23, 2012 19:43
- 0 Respostas
- 1308 Exibições
- Última mensagem por manuoliveira

Ter Out 23, 2012 19:43
Cálculo: Limites, Derivadas e Integrais
-
- comprimento do arco
por VenomForm » Seg Mai 20, 2013 13:29
- 0 Respostas
- 1239 Exibições
- Última mensagem por VenomForm

Seg Mai 20, 2013 13:29
Cálculo: Limites, Derivadas e Integrais
-
- Calculo do comprimento do arco.
por brunojorge29 » Seg Abr 23, 2012 11:21
- 3 Respostas
- 2949 Exibições
- Última mensagem por Russman

Seg Abr 23, 2012 22:32
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Comprimento de Arco
por klueger » Qui Mar 21, 2013 10:19
- 5 Respostas
- 3386 Exibições
- Última mensagem por Russman

Qui Mar 21, 2013 12:54
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





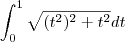
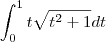
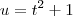
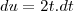

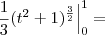
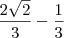

 e
e  seja
seja  . Vamos dividir esse arco em
. Vamos dividir esse arco em  pequenos intervalos
pequenos intervalos 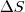 de forma que
de forma que  .
.  .
.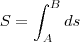 basta tomarmos
basta tomarmos  e integrar.
e integrar.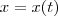 e
e  de onde
de onde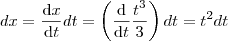
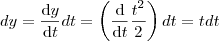
 .
. é obtido tomando
é obtido tomando  e o
e o  tomando
tomando  . Finalmente,
. Finalmente, .
.
