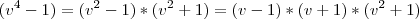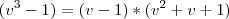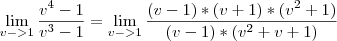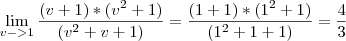por Josi » Qui Set 10, 2009 17:34
por Josi » Qui Set 10, 2009 17:34
Tenho um prova amanhã, estava estudando e não consegui resolver esa questão.
\lim_{v->1}\frac{{v}^{4}-1}{{v}^{3}-1}
Sei que o fator em comum q poderá ser simplificado é (v-1) porque ao substituirmos se der zero no numerador e no denomidor o fator que será eliminado é aquele a que o x tende com o sinal modificado, mas não consigo chegar na simplificação.
Pelo livro, a resposta é 4/3, mas não consegui chegar nela.
Por favor me ajudem!!!
-
Josi
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Set 10, 2009 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Molina » Qui Set 10, 2009 17:49
por Molina » Qui Set 10, 2009 17:49
Boa tarde, Josi.

Uma forma fácil e rápida de calcular este limite é usando L'Hopital.
Só que para usar isso você já tem que ter estudado Derivadas, o que normalmente nos cursos vem depois de Limites.
Você já estudou Derivadas? Há tópicos no próprio fórum explicando mais sobre o assunto:
search.php?st=0&sk=t&sd=d&keywords=l+hopital 
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Josi » Qui Set 10, 2009 18:07
por Josi » Qui Set 10, 2009 18:07
Não. Por enquanto tô só no limite mesmo.
A professora até falou q os repetentes q sabem não podem usar essa regra por que ela irá desconsiderar a questão.
-
Josi
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Set 10, 2009 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Molina » Qui Set 10, 2009 18:34
por Molina » Qui Set 10, 2009 18:34
Ok, Josi.
Então vamos lá:
Podemos escrever
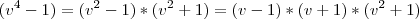
e
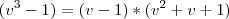
Desta forma:
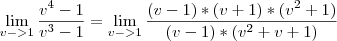
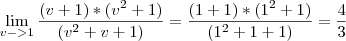
Bom estudo e boa prova!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Josi » Qui Set 10, 2009 18:40
por Josi » Qui Set 10, 2009 18:40
Muito Obrigada.
Estava fatorando errado. Agora entendi.
Valeu!!!
-
Josi
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Set 10, 2009 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4750 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- preciso de ajuda urgente!!!!
 por matematicada » Qua Nov 24, 2010 12:17
por matematicada » Qua Nov 24, 2010 12:17
- 2 Respostas
- 2066 Exibições
- Última mensagem por matematicada

Qui Nov 25, 2010 11:39
Funções
-
- preciso de ajuda, é urgente
por nayane » Sex Nov 26, 2010 21:12
- 2 Respostas
- 2020 Exibições
- Última mensagem por nayane

Sáb Nov 27, 2010 14:40
Álgebra Elementar
-
- preciso de ajuda urgente por favor
por weverton » Qua Jun 23, 2010 17:56
- 0 Respostas
- 1493 Exibições
- Última mensagem por weverton

Qua Jun 23, 2010 17:56
Matemática Financeira
-
- [Módulo] Preciso de ajuda urgente!
por natalie_ » Seg Nov 28, 2011 01:12
- 0 Respostas
- 956 Exibições
- Última mensagem por natalie_

Seg Nov 28, 2011 01:12
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.