 por Fabio Wanderley » Seg Out 22, 2012 23:37
por Fabio Wanderley » Seg Out 22, 2012 23:37
Olá,
segue a questão:
Seja f uma função par e contínua em [-r, r], r > 0. (Lembre-se: f par <--> f(- x) = f(x).)
Mostre que
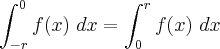 Resolução:
Resolução:u = - x
du = - dx

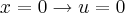
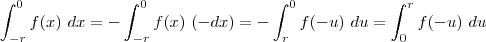
Como f é uma função par:

Mas,
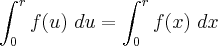
, logo:

------------
Alguém pode conferir se está certo, ou opinar sobre algo ou mesmo corrigir algum erro?
Tópico para referência:
viewtopic.php?f=120&t=9975
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por MarceloFantini » Ter Out 23, 2012 00:25
por MarceloFantini » Ter Out 23, 2012 00:25
Está correto, o raciocínio é análogo como no outro tópico.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Fabio Wanderley » Ter Out 23, 2012 00:45
por Fabio Wanderley » Ter Out 23, 2012 00:45
MarceloFantini escreveu:Está correto, o raciocínio é análogo como no outro tópico.
Obrigado!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Está certa minha resolução???
por Valmel » Qui Dez 06, 2012 00:48
- 1 Respostas
- 1900 Exibições
- Última mensagem por Valmel

Qui Dez 06, 2012 00:51
Aritmética
-
- [Função 2º grau] Minha resposta está certa?
por Richard Oliveira » Sex Mai 04, 2012 03:05
- 1 Respostas
- 1721 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 05, 2012 00:06
Funções
-
- Esta minha resolucao está correta?
por SsEstevesS » Dom Nov 27, 2011 10:29
- 0 Respostas
- 2968 Exibições
- Última mensagem por SsEstevesS

Dom Nov 27, 2011 10:29
Geometria Plana
-
- Integral definida - Resolução
por vmouc » Qui Set 01, 2011 18:03
- 4 Respostas
- 2822 Exibições
- Última mensagem por LuizAquino

Qui Set 01, 2011 18:54
Cálculo: Limites, Derivadas e Integrais
-
- [Resolução de Integral Definida]
por Seza Saenz » Qui Mar 24, 2016 15:18
- 0 Respostas
- 2001 Exibições
- Última mensagem por Seza Saenz

Qui Mar 24, 2016 15:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
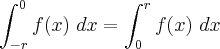

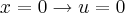
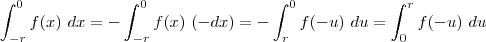

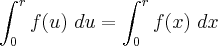 , logo:
, logo:






 , avisa que eu resolvo.
, avisa que eu resolvo.

