segue o exercício
Um aluno, ao calcular a integral
![\int_{-1}^{1}\sqrt[]{1+x^2}dx](/latexrender/pictures/5f67c95a6257ba5c4a4fd83801628a36.png "\int_{-1}^{1}\sqrt[]{1+x^2}dx")
, raciocinou da seguinte forma: fazendo a mudança de variável 
, os novos extremos de integração seriam iguais a 2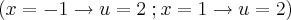 
e assim a integral obtida após a mudança de variável seria igual a zero e, portanto, ![\int_{-1}^{1}\sqrt[]{1+x^2} \ dx=0](/latexrender/pictures/0ec803b84ab00e3af1771e750fa800a1.png "\int_{-1}^{1}\sqrt[]{1+x^2} \ dx=0")
.Onde está o erro?
-------------------
Bom, se os intervalos de integração são os mesmo, a integral não deveria ser igual a zero??
De qualquer forma, fazendo o que o aluno fez e derivando a variável "u", eu cheguei a isso:
![\int_{2}^{2}\sqrt[]{u} \ 2x \ dx](/latexrender/pictures/95d78d66aa1f4faf25411c57e5dbf30b.png "\int_{2}^{2}\sqrt[]{u} \ 2x \ dx")
O fato de ter a variável "u" com "x dx" no integrando deixa a resolução errada?
.
