Os valores de m e k para que as equações do sistema
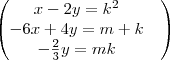
representem uma única reta são, respectivamente:
a) ?(2/9) e ?(2/3).
b) ?(2/3) e 2/3.
c) ?(3/2) e ?(2/3).
d) (2/9) e (2/9).
1º - Tentei resolver por tentativa, mas foi muito trabalhoso e não cheguei ao resultado
2º - Coloquei esses valores no geogebra, só dá erro, isso é função inválida.
Desde já agradeço a ajuda de todos
Obrigado


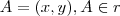 . Isolando o "y" em cada equação , por exemplo . Você tem o ponto A em função de x , m e k para todo x real . Para x = 0 por exemplo ,podemos estabelecer uma igualdade que implicará uma condição para m e k que satisfaça as três equações .
. Isolando o "y" em cada equação , por exemplo . Você tem o ponto A em função de x , m e k para todo x real . Para x = 0 por exemplo ,podemos estabelecer uma igualdade que implicará uma condição para m e k que satisfaça as três equações . 
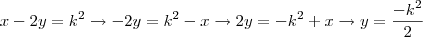
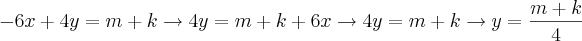
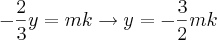
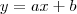 . Onde
. Onde 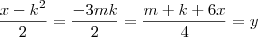 .
. 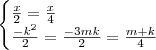 . Daí, podemos estabelcer que ,
. Daí, podemos estabelcer que ,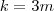 .
. 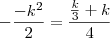 .
.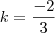
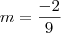 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)