a) 90º
b) 87º
c) 270º
d) 277,5º
e) 272º 30'
Lá vai minha resolução: (Desculpe pela precariedade da imagem uhsahuas.. mas n consegui desenhar e peguei esse relogio e editei)
Como ele disse que quando marca 3 horas o ângulo que se forma é 90º, então cada hora é 30º
Calculando o angulo azul que eu chamei de z
60 min -------- 30º
15 min -------- z .:. z = 7º30'
Bem do ponteiro 12 ao 15 temos 3 horas, que vai ser o total (chamei de t)
60 min -------- 30º
180 min ------- T .:. T = 90º
Para achar o angulo vermelho (verde + azul = total)
z + v = T
7º30' + v = 90º .:. v = 82º30'
Sendo que essa opção nem tem no no gabarito.
E o gabarito >> D) 277,5º
Alguém poderia explicar oq eu fiz errado ? :\
Obrigado :]
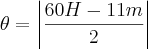
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.