por Danilo Dias Vilela » Qui Set 10, 2009 14:53
Gostaria que me ajudassem na seguinte questão: 1) O sistema ax-2y=1, bx+4y=5 tem solução determinada, somente se:
a)
b)
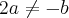
c)
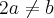
d)a= -2b (menos dois b)
e)a=b
Tenho tentado dar valores para a e para b, mas não tô conseguindo. Se alguém puder me ajudar. Já me responderam este tópico, mas por determinante. Gostaria de saber se não há outro modo melhor de fazer este exercício, pois ainda não vi determinantes. Molina se você ver de novo e puder me explicar uma outra forma de fazer ficaria muito grato.
-
Danilo Dias Vilela
- Usuário Dedicado
-
- Mensagens: 45
- Registrado em: Qua Set 09, 2009 01:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
por Elcioschin » Qui Set 10, 2009 15:20
ax - 2y = 1 ----> Multiplicando por 2 ----> 2ax - 2y = 2 ----> Equação I
bx + 4y = 5 ----> Equação II
Somando I e II -----> 2ax + bx = 2 + 5 -----> (2a + b)*x = 7 ----> x = 7/(2a + b)
Para existir x, o denominador do 2° membro NÃO pode ser nulo ----> 2a + b <> 0 ----> 2a <> - b ----> B
Obs.: o sinal <> significa "diferente".
-
Elcioschin
- Colaborador Voluntário
-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- sistemas de equãções
por Rejane Sampaio » Sex Set 12, 2008 23:54
- 1 Respostas
- 2662 Exibições
- Última mensagem por admin
Ter Set 16, 2008 20:31
Estatística
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 17:34
- 1 Respostas
- 1274 Exibições
- Última mensagem por Molina
Qua Set 09, 2009 17:54
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 21:19
- 1 Respostas
- 1435 Exibições
- Última mensagem por Elcioschin
Qua Set 09, 2009 22:27
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 23:55
- 1 Respostas
- 2299 Exibições
- Última mensagem por Molina
Qui Set 10, 2009 14:15
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qui Set 10, 2009 00:25
- 2 Respostas
- 2264 Exibições
- Última mensagem por RICI
Sex Ago 24, 2012 11:58
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
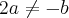
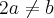
