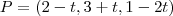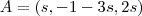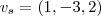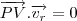exemplo 1)
a reta pode ser escrita como

sendo asssim o vetor diretor da reta é v=(1,-2,-2)
pegando um ponto A qualquer da reta podemos construir o vetor
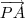
, este vetor pode ser decomposto em dois vetores um na direção da reta e outro ortogonal a este, sendo que o modulo deste vetor ortogonal nos fornece a menor distancia entre o ponto e a reta.
seu modulo pode ser fornecido por
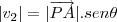
em que

é o angulo entre o vetor PA e o vetor direção da reta mais temos que
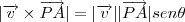
então a distancia pode ser calculada por

onde v é o vetor direção da reta, P é o ponto dado, e A é um ponto qualquer pertencente a reta.
B) se a reta é paralela ao plano, então o vertor diretor da reta tem que ser ortogonal ao vetor normal ao plano, isto tem que ser verificado antes de calcular, caos contrario a reta intercepta o plano e a distancia é igual a 0.
a distancia de uma reta a um plano pode ser calculada pegando um ponto qualquer da reta e calculando a distancia desse ponto até o plano.
primeiro encontramos um ponto P qualquer da e um ponto A qualquer do plano e assim temos um vetor PA
a distancia sera calculada como sendo a projeção deste vetor sobre o vetor normal ao plano ou seja:
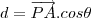
em que

é o angulo entre o vetor normal e o vetor PA
temos que
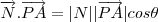
então a distancia é dada por
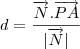
C)
primeiro é necessaria encontrar o vetor que seja normal as duas retas, fazendo o produto vetorial entre os dois vetores diretores de cada reta.
escolhendo um ponto P em uma reta e um ponto A na outra reta temos o vetor PA, a distancia entre as retas pode ser calculada pela projeção desse vetor PA sobre o vetor normal as duas retas.
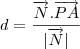
 : y=0
: y=0


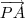 , este vetor pode ser decomposto em dois vetores um na direção da reta e outro ortogonal a este, sendo que o modulo deste vetor ortogonal nos fornece a menor distancia entre o ponto e a reta.
, este vetor pode ser decomposto em dois vetores um na direção da reta e outro ortogonal a este, sendo que o modulo deste vetor ortogonal nos fornece a menor distancia entre o ponto e a reta.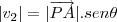
 é o angulo entre o vetor PA e o vetor direção da reta mais temos que
é o angulo entre o vetor PA e o vetor direção da reta mais temos que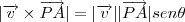

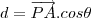
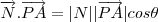
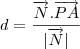

![\sqrt[2]{(x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2} \sqrt[2]{(x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2}](/latexrender/pictures/5de41ab8e88d04047a429625e17d7b61.png)
![\sqrt[2]{ 4/3 + 49/3 + 64/3} \sqrt[2]{ 4/3 + 49/3 + 64/3}](/latexrender/pictures/3874f94f7b0d636dcbb66f193c1e6c6b.png)
![\sqrt[2]{117/3} \sqrt[2]{117/3}](/latexrender/pictures/28366d8a2977fe4dc8afa620cabe6df2.png)