 por barbara-rabello » Qui Out 18, 2012 12:22
por barbara-rabello » Qui Out 18, 2012 12:22
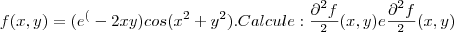
Consegui calcular a derivada primeira em x:
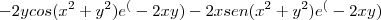
E a derivada primeira em y:
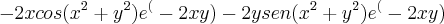
Tenho as respostas das derivadas segundas, mas n´~ao estou conseguindo calculá-las, pois são expressões longas
com vários produtos, não consegui derivar tudo!!
Alguém pode me ajudar?
Derivada segunda em x:
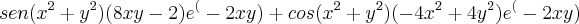
derivada segunda em y:
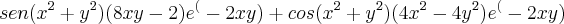
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por barbara-rabello » Qui Out 18, 2012 12:23
por barbara-rabello » Qui Out 18, 2012 12:23
Na questão é e^(-2xy), não consegui ajeitar no editor, desculpem!
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por young_jedi » Qui Out 18, 2012 16:32
por young_jedi » Qui Out 18, 2012 16:32
partindo da derivada primeira que voce ja calculou
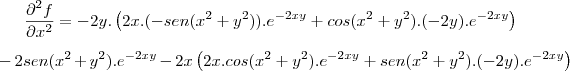
fazendo as multiplicações
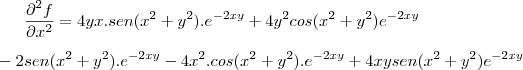
resolvendo as somas
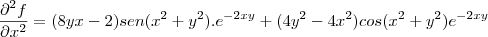
tente fazer para a derivada segunda de y
Dicas: na hora de fazer exponecial o expoente tem que ficar entre chaves e^{-2xy}
e na derivada parcial voce deve ter feito no denominador \partialx, mas tem que ter um espaço entre o x
\partial x ou \partial y
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por e8group » Qui Out 18, 2012 18:20
por e8group » Qui Out 18, 2012 18:20
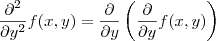
Como,
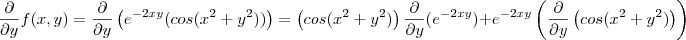
![\frac{\partial }{\partial y}f(x,y) = -2e^{-2xy}\left[ ysin(x^2+y^2)+x(cos(x^2+y^2)) \right ] . \frac{\partial }{\partial y}f(x,y) = -2e^{-2xy}\left[ ysin(x^2+y^2)+x(cos(x^2+y^2)) \right ] .](/latexrender/pictures/a9315b845a009924bf83f392af36d003.png)
Assim ,
![\frac{\partial^2 }{\partial y^2}f(x,y) = \frac{\partial }{\partial y}\left(-2e^{-2xy}\left[ ysin(x^2+y^2)+x(cos(x^2+y^2)) \right ]\right) \frac{\partial^2 }{\partial y^2}f(x,y) = \frac{\partial }{\partial y}\left(-2e^{-2xy}\left[ ysin(x^2+y^2)+x(cos(x^2+y^2)) \right ]\right)](/latexrender/pictures/62dd5124a8541e81dd372396759baa33.png)
.
Agora seja ,
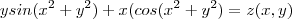
.
![\frac{\partial^2 }{\partial y^2}f(x,y) = -2 \frac{\partial }{\partial y}\left(e^{-2xy}\cdot z(x,y) \right) = -2 \left( z(x,y)\left[\frac{\partial }{\partial y}e^{-2xy} \right ] +e^{-2xy}\left[\frac{\partial }{\partial y}z(x,y) \right ]\right ) \frac{\partial^2 }{\partial y^2}f(x,y) = -2 \frac{\partial }{\partial y}\left(e^{-2xy}\cdot z(x,y) \right) = -2 \left( z(x,y)\left[\frac{\partial }{\partial y}e^{-2xy} \right ] +e^{-2xy}\left[\frac{\partial }{\partial y}z(x,y) \right ]\right )](/latexrender/pictures/11fc44a260833d7ded4ff8f504e74781.png)
.
Derivando por partes ,
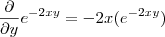
e
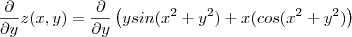
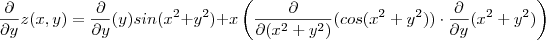
![\frac{\partial }{\partial y}z(x,y) = sin(x^2+y^2 ) + 2y^2 cos (x^2+y^2) - 2xy sin(x^2+y^2) = sin(x^2 +y^2 )[ 1 -2xy] + 2y^2 cos(x^2+y^2) \frac{\partial }{\partial y}z(x,y) = sin(x^2+y^2 ) + 2y^2 cos (x^2+y^2) - 2xy sin(x^2+y^2) = sin(x^2 +y^2 )[ 1 -2xy] + 2y^2 cos(x^2+y^2)](/latexrender/pictures/73c423bd0b2cec417a5c5f3f4adf6f3d.png)
Fazendo as substituições , obteremos que :
![\frac{\partial^2 }{\partial y^2}f(x,y) = -2e^{-2xy}([-2xysin(x^2+y^2)-2x^2(cos(x^2+y^2)] + sin(x^2 +y^2 )[ 1 -2xy] + 2y^2 cos(x^2+y^2) ) \frac{\partial^2 }{\partial y^2}f(x,y) = -2e^{-2xy}([-2xysin(x^2+y^2)-2x^2(cos(x^2+y^2)] + sin(x^2 +y^2 )[ 1 -2xy] + 2y^2 cos(x^2+y^2) )](/latexrender/pictures/b1f2dd18d7fc6566248908faac2ab729.png)
![\frac{\partial^2 }{\partial y^2}f(x,y) = -2e^{-2xy}(sin(x^2+y^2)[1-4xy] + cos(x^2+y^2)[2y^2-2x^2]) \frac{\partial^2 }{\partial y^2}f(x,y) = -2e^{-2xy}(sin(x^2+y^2)[1-4xy] + cos(x^2+y^2)[2y^2-2x^2])](/latexrender/pictures/8ab03b4f0106d8c26d0dc5b6ce9646c6.png)

![\frac{\partial^2 }{\partial y^2}f(x,y) = sin(x^2+y^2)[8xy-2]e^{-2xy} + cos(x^2+y^2)[4x^2-4y^2]e^{-2xy} \frac{\partial^2 }{\partial y^2}f(x,y) = sin(x^2+y^2)[8xy-2]e^{-2xy} + cos(x^2+y^2)[4x^2-4y^2]e^{-2xy}](/latexrender/pictures/b1303a1fa7262716e522b313109e416d.png)
OBS.: Recomendo este site :
http://www.codecogs.com/latex/eqneditor.php?lang=pt-br para visualizar o latex antes de postar aqui .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- segunda derivada
por jmario » Sex Mai 07, 2010 22:25
- 2 Respostas
- 2708 Exibições
- Última mensagem por Molina

Sáb Mai 08, 2010 14:00
Cálculo: Limites, Derivadas e Integrais
-
- [derivada segunda]
por nayra suelen » Qua Mai 30, 2012 13:38
- 2 Respostas
- 1638 Exibições
- Última mensagem por nayra suelen

Qua Mai 30, 2012 14:42
Cálculo: Limites, Derivadas e Integrais
-
- Derivada da primeira e derivada da segunda
por Laisa » Ter Fev 26, 2019 17:02
- 1 Respostas
- 5688 Exibições
- Última mensagem por DanielFerreira

Qui Set 05, 2019 23:28
Cálculo: Limites, Derivadas e Integrais
-
- Derivada primeira e segunda
por luiz3107 » Ter Ago 17, 2010 16:39
- 2 Respostas
- 2928 Exibições
- Última mensagem por luiz3107

Ter Ago 17, 2010 17:54
Cálculo: Limites, Derivadas e Integrais
-
- derivada de segunda ordem
por lgbmp » Sex Set 03, 2010 19:25
- 2 Respostas
- 3033 Exibições
- Última mensagem por lgbmp

Seg Set 06, 2010 13:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
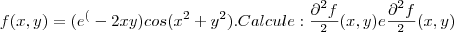
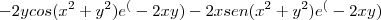
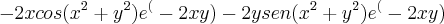
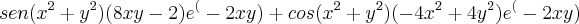
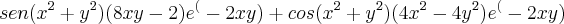


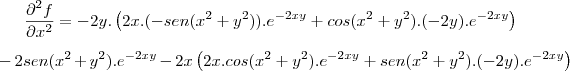
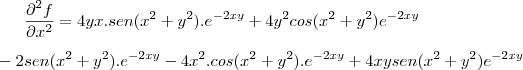
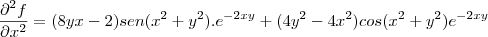

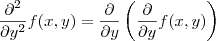
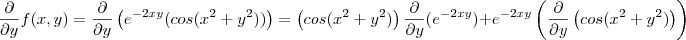
![\frac{\partial }{\partial y}f(x,y) = -2e^{-2xy}\left[ ysin(x^2+y^2)+x(cos(x^2+y^2)) \right ] . \frac{\partial }{\partial y}f(x,y) = -2e^{-2xy}\left[ ysin(x^2+y^2)+x(cos(x^2+y^2)) \right ] .](/latexrender/pictures/a9315b845a009924bf83f392af36d003.png)
![\frac{\partial^2 }{\partial y^2}f(x,y) = \frac{\partial }{\partial y}\left(-2e^{-2xy}\left[ ysin(x^2+y^2)+x(cos(x^2+y^2)) \right ]\right) \frac{\partial^2 }{\partial y^2}f(x,y) = \frac{\partial }{\partial y}\left(-2e^{-2xy}\left[ ysin(x^2+y^2)+x(cos(x^2+y^2)) \right ]\right)](/latexrender/pictures/62dd5124a8541e81dd372396759baa33.png) .
. 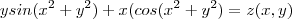 .
. ![\frac{\partial^2 }{\partial y^2}f(x,y) = -2 \frac{\partial }{\partial y}\left(e^{-2xy}\cdot z(x,y) \right) = -2 \left( z(x,y)\left[\frac{\partial }{\partial y}e^{-2xy} \right ] +e^{-2xy}\left[\frac{\partial }{\partial y}z(x,y) \right ]\right ) \frac{\partial^2 }{\partial y^2}f(x,y) = -2 \frac{\partial }{\partial y}\left(e^{-2xy}\cdot z(x,y) \right) = -2 \left( z(x,y)\left[\frac{\partial }{\partial y}e^{-2xy} \right ] +e^{-2xy}\left[\frac{\partial }{\partial y}z(x,y) \right ]\right )](/latexrender/pictures/11fc44a260833d7ded4ff8f504e74781.png) .
. 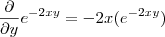 e
e 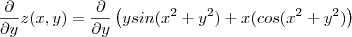
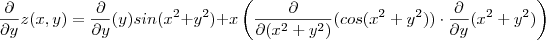
![\frac{\partial }{\partial y}z(x,y) = sin(x^2+y^2 ) + 2y^2 cos (x^2+y^2) - 2xy sin(x^2+y^2) = sin(x^2 +y^2 )[ 1 -2xy] + 2y^2 cos(x^2+y^2) \frac{\partial }{\partial y}z(x,y) = sin(x^2+y^2 ) + 2y^2 cos (x^2+y^2) - 2xy sin(x^2+y^2) = sin(x^2 +y^2 )[ 1 -2xy] + 2y^2 cos(x^2+y^2)](/latexrender/pictures/73c423bd0b2cec417a5c5f3f4adf6f3d.png)
![\frac{\partial^2 }{\partial y^2}f(x,y) = -2e^{-2xy}([-2xysin(x^2+y^2)-2x^2(cos(x^2+y^2)] + sin(x^2 +y^2 )[ 1 -2xy] + 2y^2 cos(x^2+y^2) ) \frac{\partial^2 }{\partial y^2}f(x,y) = -2e^{-2xy}([-2xysin(x^2+y^2)-2x^2(cos(x^2+y^2)] + sin(x^2 +y^2 )[ 1 -2xy] + 2y^2 cos(x^2+y^2) )](/latexrender/pictures/b1f2dd18d7fc6566248908faac2ab729.png)
![\frac{\partial^2 }{\partial y^2}f(x,y) = -2e^{-2xy}(sin(x^2+y^2)[1-4xy] + cos(x^2+y^2)[2y^2-2x^2]) \frac{\partial^2 }{\partial y^2}f(x,y) = -2e^{-2xy}(sin(x^2+y^2)[1-4xy] + cos(x^2+y^2)[2y^2-2x^2])](/latexrender/pictures/8ab03b4f0106d8c26d0dc5b6ce9646c6.png)

![\frac{\partial^2 }{\partial y^2}f(x,y) = sin(x^2+y^2)[8xy-2]e^{-2xy} + cos(x^2+y^2)[4x^2-4y^2]e^{-2xy} \frac{\partial^2 }{\partial y^2}f(x,y) = sin(x^2+y^2)[8xy-2]e^{-2xy} + cos(x^2+y^2)[4x^2-4y^2]e^{-2xy}](/latexrender/pictures/b1303a1fa7262716e522b313109e416d.png)





