 por manuoliveira » Qua Out 17, 2012 21:40
por manuoliveira » Qua Out 17, 2012 21:40
Estou estudando integrais por frações parciais mas travei na seguinte:
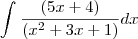
Tenho prova semana que vem então agradeço mesmo quem puder ajudar!! Obrigada desde já
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por MarceloFantini » Qua Out 17, 2012 22:43
por MarceloFantini » Qua Out 17, 2012 22:43
Segundo o
Wolfram Alpha, a expansão em frações parciais será

.
Agora basta integrar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Qui Out 18, 2012 11:10
por e8group » Qui Out 18, 2012 11:10
Visto que ,

.
Temos que ,
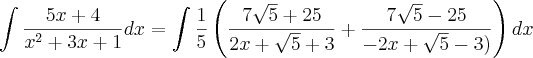
.
Escrevendo esta integral indefinida (antiderivada) como ,
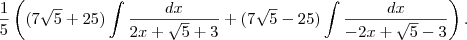
Integrando cada termo ,obtemos que :
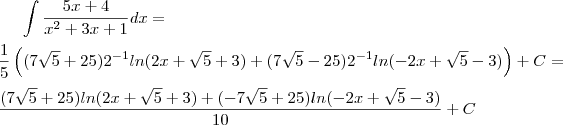
OBS.: Se eu errei alguma "passagem " (ainda não vi este conteúdo ,resolvir por curiosidade),post aí por favor .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- como resolver a integral de y² . e^y²
por Anniinha » Ter Ago 16, 2011 18:57
- 10 Respostas
- 6138 Exibições
- Última mensagem por LuizAquino

Qua Ago 17, 2011 17:25
Cálculo: Limites, Derivadas e Integrais
-
- Duvida de como resolver integral
por Manoella » Qui Fev 24, 2011 22:51
- 1 Respostas
- 1847 Exibições
- Última mensagem por LuizAquino

Dom Fev 27, 2011 19:23
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver essa integral.
por 380625 » Qua Set 07, 2011 14:02
- 3 Respostas
- 3108 Exibições
- Última mensagem por Neperiano

Qua Set 07, 2011 15:37
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida. Como resolver?
por Cristiano Tavares » Sex Nov 25, 2011 22:54
- 4 Respostas
- 3048 Exibições
- Última mensagem por Cristiano Tavares

Qua Nov 30, 2011 15:32
Cálculo: Limites, Derivadas e Integrais
-
- Integral Iterada - Como resolver?
 por Cleyson007 » Qua Abr 18, 2012 16:44
por Cleyson007 » Qua Abr 18, 2012 16:44
- 4 Respostas
- 2354 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 21, 2012 17:00
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
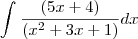

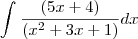



 .
. 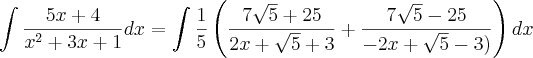 .
.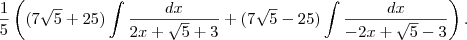
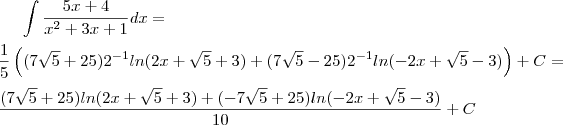

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.