 por barbara-rabello » Seg Out 15, 2012 20:40
por barbara-rabello » Seg Out 15, 2012 20:40
Seja a função f(x,y,z) abaixo:
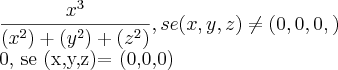
e

=
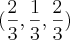
Como calculo a derivada direcional fora da origem?
Só consegui calcular na origem (usando a definição de derivada) e achei

como resposta,
mas não sei como calcular fora da origem.
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por MarceloFantini » Seg Out 15, 2012 21:57
por MarceloFantini » Seg Out 15, 2012 21:57
A derivada direcional é definida como
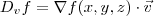
, ou seja, a projeção do gradiente na direção do vetor

. Não sei como você calculou na origem, mas o enunciado não parece estar completo. Qual é o ponto que você quer encontrar a derivada direcional?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por barbara-rabello » Ter Out 16, 2012 16:39
por barbara-rabello » Ter Out 16, 2012 16:39
O enunciado é só isso mesmo, ele não fala de ponto.
Na origem
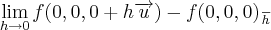
,
que fica f

Me desculpa, o vetor certo é:

-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por barbara-rabello » Ter Out 16, 2012 16:40
por barbara-rabello » Ter Out 16, 2012 16:40
Me desculpem, na fórmula do limite, aquele 'h' com risco em cima é na verdade o denominador, saiu errado!!
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por young_jedi » Ter Out 16, 2012 19:37
por young_jedi » Ter Out 16, 2012 19:37
talvez o exercicio so peça para calcular o produto escalar do vetor gradiente pelo vetor

, e deixar em função de x, y e z, para encontrar a derivada direcional em qualquer ponto seria so substituir os pontos dai.
Se voce quiser colocar o enunciado exatamente como ele esta para agente dar uma olhada...
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por barbara-rabello » Qua Out 17, 2012 12:47
por barbara-rabello » Qua Out 17, 2012 12:47
Então, o enunciado é esse:
Seja a função f(x,y,z) abaixo:
![\frac{x^3}{x^2+y^2+z^2}, se (x,y,z) [tex]\neq (0,0,0) \frac{x^3}{x^2+y^2+z^2}, se (x,y,z) [tex]\neq (0,0,0)](/latexrender/pictures/679d768f74432e961f6c64f8301a6148.png)
0, se (x,y,z) = (0,0,0)
e

Calcule
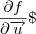
para (xo,yo,zo)[\tex] \neq[\tex] 0.
Calcule
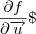
(0,0,0)
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por barbara-rabello » Qua Out 17, 2012 12:47
por barbara-rabello » Qua Out 17, 2012 12:47
Me desculpem, aparedeu um cifrão nas derivadas que não tem!!
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por young_jedi » Qua Out 17, 2012 19:48
por young_jedi » Qua Out 17, 2012 19:48
Barbara-rabello
acho que é isso mesmo, o exercicio so pede pra voce calcular o produto escalar do vetor gradiente pelo vetor direção e deixar em função de x,y e z
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por barbara-rabello » Qui Out 18, 2012 12:03
por barbara-rabello » Qui Out 18, 2012 12:03
É isso mesmo, já consegui fazer. Obrigada pela ajuda!!!!
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada Direcional
por bruuno » Seg Nov 25, 2013 16:45
- 1 Respostas
- 1796 Exibições
- Última mensagem por Bravim

Ter Nov 26, 2013 03:20
Cálculo: Limites, Derivadas e Integrais
-
- Derivada Direcional
por Renan1434 » Ter Dez 16, 2014 16:00
- 1 Respostas
- 1649 Exibições
- Última mensagem por adauto martins

Qua Dez 17, 2014 15:39
Cálculo: Limites, Derivadas e Integrais
-
- Derivada direcional
 por Jadiel Carlos » Seg Nov 21, 2016 11:14
por Jadiel Carlos » Seg Nov 21, 2016 11:14
- 2 Respostas
- 5874 Exibições
- Última mensagem por Jadiel Carlos

Qui Nov 24, 2016 01:16
Cálculo: Limites, Derivadas e Integrais
-
- [Gradiente e derivada direcional]
por dulifs » Seg Out 31, 2011 15:22
- 2 Respostas
- 4884 Exibições
- Última mensagem por dulifs

Seg Out 31, 2011 18:14
Cálculo: Limites, Derivadas e Integrais
-
- Questão de derivada direcional e gradiente
por Cristiano Tavares » Dom Mai 29, 2011 11:25
- 2 Respostas
- 3801 Exibições
- Última mensagem por Cristiano Tavares

Dom Mai 29, 2011 19:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
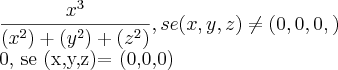
 =
= 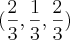
 como resposta,
como resposta,
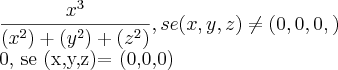
 =
= 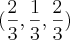
 como resposta,
como resposta,
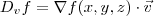 , ou seja, a projeção do gradiente na direção do vetor
, ou seja, a projeção do gradiente na direção do vetor  . Não sei como você calculou na origem, mas o enunciado não parece estar completo. Qual é o ponto que você quer encontrar a derivada direcional?
. Não sei como você calculou na origem, mas o enunciado não parece estar completo. Qual é o ponto que você quer encontrar a derivada direcional?




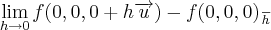 ,
,



 , e deixar em função de x, y e z, para encontrar a derivada direcional em qualquer ponto seria so substituir os pontos dai.
, e deixar em função de x, y e z, para encontrar a derivada direcional em qualquer ponto seria so substituir os pontos dai.
![\frac{x^3}{x^2+y^2+z^2}, se (x,y,z) [tex]\neq (0,0,0) \frac{x^3}{x^2+y^2+z^2}, se (x,y,z) [tex]\neq (0,0,0)](/latexrender/pictures/679d768f74432e961f6c64f8301a6148.png)

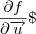 para (xo,yo,zo)[\tex] \neq[\tex] 0.
para (xo,yo,zo)[\tex] \neq[\tex] 0.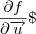 (0,0,0)
(0,0,0)



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.