[Equação de planos] Dùvida exercício 8

[MrJuniorFerr]

Estou com mais uma dúvida, só que agora no seguinte exercício:

Deduza uma equação do plano definido pelo eixo z e pelo ponto P(4,4,1).
Gabarito:

Resolvi da seguinte forma:
Por o plano estar definido pelo eixo z, imaginei que o vetor v=(0,0,1) fosse pertencente ao plano.
Como o vetor normal do plano é perpendicular a este vetor v, sei que .

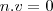Então







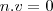
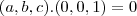
Então achei o vetor normal ao plano n=(0,0,1)

Achando o valor de d:





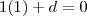
Colocando o vetor normal e d na equação:





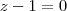
Como podem ver o meu resultado deu diferente do gabarito...
Minha resolução está certa?

[young_jedi]

o vetor normal ao plano não é (0,0,1)
é (a,b,c) como voce achou que c=0
então o vetor normal é (a,b,0)

como o plano é definido pelo eixo z então qualquer ponto do eixo z pertence ao plano
por isso pegue algum destes pontos e diga que este ponto é C (sugiro o ponto (0,0,0) para facilitar nos calculos), encontre o vetor PC, sendo que o produto vetorial



dara o vetor normal ao plano, com isso voce determina a equação do plano.

[MarceloFantini]

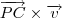
Jedi, a notação usual de produto vetorial é ou 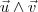. A notação que você usou é a de produto tensorial.

[MrJuniorFerr]

Pelo que eu entendi... quando o plano for paralelo ao eixo z, poderemos utilizar o vetor v=(0,0,1).
E quando um plano for definido pelo eixo z, poderemos utilizar o vetor v=(1,1,0)

[young_jedi]

tanto quando o plano for paralelo quando o vetor for definido o vetor normal ao plano é do tipo (a,b,0)
e nos dois casos nos podemos utilizar o vetor (0,0,1) para encontrar o vetor normal, so que quando o plano é definido pelo eixo z os pontos que estão sobre o eixo z podem ser utilizados (0,0,z) para encontrar outro vetor em um plano paralelo não, pois estes pontos não pertencem ao plano

[MrJuniorFerr]

o vetor normal ao plano não é (0,0,1)
é (a,b,c) como voce achou que c=0
então o vetor normal é (a,b,0)

como o plano é definido pelo eixo z então qualquer ponto do eixo z pertence ao plano
por isso pegue algum destes pontos e diga que este ponto é C (sugiro o ponto (0,0,0) para facilitar nos calculos), encontre o vetor PC, sendo que o produto vetorial



dara o vetor normal ao plano, com isso voce determina a equação do plano.

Então eu só preciso pegar um ponto, por exemplo, C(0,0,1) do eixo z, fazer o vetor CP ou PC e fazer produto vetorial CP x CP ou PC x PC? Não sabia q dava pra fazer produto vetorial do mesmo vetor e achar um vetor perpendicular a ele... eu achava que tinha que ter 2 vetores diferentes coplanares.

[young_jedi]

Na verdade voce precisa pegar dois pontos do eixo z
por esemplo C(0,0,1) e O(0,0,0) e ai fazer o produto vetorial PO x CO para encontrar o vetor normal eu digitei errado anteriormente vou corrigir, desculpa ai.O que voce disse esta correto precisa ser dois vetores coplanares

[MrJuniorFerr]

O que me anda confundindo muito são os seguintes exercícios:

Escreva uma equação do plano paralelo ao eixo z e que contém os pontos (2,0,0) e (0,3,2). Gabarito:

Escreva uma equação do plano paralelo ao eixo z que contém o ponto (1,1,1). Gabarito:

Como pode ver, nos dois exercícios o plano é paralelo ao eixo z e olha como as equações no gabarito são totalmente diferentes! :x
E o resultados do gabarito estão certos, pois confirmei com uma colega.

[young_jedi]

o que acontece é que podem ter infinitos planos paralelos ao exio z, a unica coisa que eles tem em comum é que o vetor normal deles é ortogonal ao eixo z.
no primeiro caso por exemplo voce pode pegar os pontos A(2,0,0) e B(0,3,2) encontra vetor AB e fazer o produto vetorial com o vetor (0,0,1) ai voce encontra o vetor normal ao plano.

A segundo caso acho estranho o resultado ter dado z=1 pois este plano é ortogonal ao eixo z e não paralelo, a resposta poderia ser x=1 ou então y=1 este dois planos são soluções para a questão mais o plano z=1 não, sugiro que voce verifique esta questão com o professor ou então de alguma fonte onde ela foi retirada.

[MarceloFantini]

Escreva uma equação do plano paralelo ao eixo z que contém o ponto (1,1,1). Gabarito:

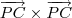
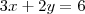
Este plano não é paralelo ao eixo z, e sim ortogonal. Ele é paralelo ao plano , ou paralelo aos eixos x e y simultaneamente. Essa pergunta contém uma contradição: não é possível ser paralelo ao eixo se cortá-lo.

[MrJuniorFerr]

Mandei um e-mail pra minha professora a respeito desse exercício. só me resta aguardar...
Irei dormir e 5:15h da manhã estarei de volta para a luta. haha
A minha lista têm 31 exercícios, eu já a terminei. Mas como ela deve também ser entregue, estou juntamente refazendo-a e passando a limpo. Estou com dúvidas nesses exercícios pq vc jedi, tinha me ensinado a fazer pelo método divindindo a equação geral do plano por a, etc. Mas, quero dominar a forma convencional para resolve-los.
Obrigado pela grande ajuda Marcelo e Jedi. Eu jamais teria terminado essa lista sem a ajuda de vocês, muitas dúvidas ficariam para trás.