 por Danilo » Sáb Out 13, 2012 16:03
por Danilo » Sáb Out 13, 2012 16:03
Ache Y x (
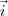
+
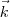
) = 2(
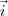
+
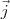
-
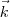
) e
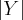
=
![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png)
aqui essa barra representa a Norma de Y, pois eu não encontrei a ''barra dupla''. E ''x'' é o produto vetorial.
Bom, inicialmente eu substitui os vetores canônicos pelas suas respectivas componentes. Mas eu não consigo relacionar a norma com o produto vetorial... esse é o problema. Grato a quem puder dar uma luz!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Sáb Out 13, 2012 17:05
por MarceloFantini » Sáb Out 13, 2012 17:05
Seja
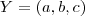
. Então
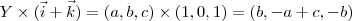
, que por hipótese segue que
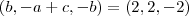
.
Assim,

e

, portanto o vetor

será

.
Agora usamos a informação que

. Sabemos que

, então

,

e

, portanto

.
Finalmente, concluímos que

. Você pode verificar fazendo

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- norma de um vetor
por nandooliver008 » Qua Nov 12, 2014 00:51
- 1 Respostas
- 1105 Exibições
- Última mensagem por adauto martins

Qua Nov 12, 2014 11:38
Geometria Analítica
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4946 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
-
- Vetor e Produto Escalar
 por camposhj » Ter Set 20, 2011 22:10
por camposhj » Ter Set 20, 2011 22:10
- 9 Respostas
- 20711 Exibições
- Última mensagem por camposhj

Qua Set 28, 2011 22:06
Geometria Analítica
-
- Espaço vetorial - Vetor nulo
por Razoli » Qua Mar 18, 2015 19:03
- 0 Respostas
- 1154 Exibições
- Última mensagem por Razoli

Qua Mar 18, 2015 19:03
Álgebra Linear
-
- Produto Vetorial
por ARCS » Sex Mai 20, 2011 08:59
- 1 Respostas
- 2359 Exibições
- Última mensagem por LuizAquino

Sex Mai 20, 2011 10:25
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
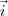 +
+ 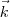 ) = 2(
) = 2(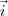 +
+ 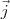 -
- 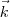 ) e
) e 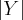 =
= ![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png) aqui essa barra representa a Norma de Y, pois eu não encontrei a ''barra dupla''. E ''x'' é o produto vetorial.
aqui essa barra representa a Norma de Y, pois eu não encontrei a ''barra dupla''. E ''x'' é o produto vetorial. 

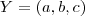 . Então
. Então 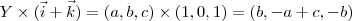 , que por hipótese segue que
, que por hipótese segue que 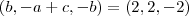 .
.  e
e  , portanto o vetor
, portanto o vetor  será
será  .
.  . Sabemos que
. Sabemos que  , então
, então  ,
,  e
e  , portanto
, portanto  .
. . Você pode verificar fazendo
. Você pode verificar fazendo  .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.