 por Sobreira » Sáb Out 13, 2012 00:07
por Sobreira » Sáb Out 13, 2012 00:07
![f (x) \lim_{4-}\frac{\sqrt[]{16-{x}^{2}}}{x-4} f (x) \lim_{4-}\frac{\sqrt[]{16-{x}^{2}}}{x-4}](/latexrender/pictures/ce6d42505c105a7702d299f740a0fa83.png)
Vendo este limite.
Bom, a técnica que eu utilizo para resolver é que, se tratando de um limite genérico eu substituo o valor de x para o qual está tendendo a função (4).
Neste caso, com a substituição surgirá uma indeterminação do tipo 0/0, então eu sei que tenho que fatorar este polinômio para efetuar os cálculos.
Minha dúvida é, se para quando eu efetuar uma substituição e o numerador der uma constante e o denominador zero, para análise do sinal do infinito, eu devo fatorar o denominador sempre??
Ex.
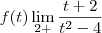
Nestes casos que o numerador der uma constante e o denominador der zero direto com a substituição eu devo fatorar o denominador ou posso fazer direto considerando valores maiores que 2 (Por Ex. 3)?
Editado pela última vez por
Sobreira em Sáb Out 13, 2012 01:32, em um total de 1 vez.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MrJuniorFerr » Sáb Out 13, 2012 00:50
por MrJuniorFerr » Sáb Out 13, 2012 00:50
Em Limites infinitos, ou seja, quando o numerador der diferente de 0 de primeira, não é necessário fatorar o denominador. Neste exemplo que você citou, sabe-se que substituindo o valor de t no numerador, será uma constante positiva e como t tende a
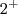
, substituindo 2,01 em t no denominador, você obtém um valor maior que zero, ou seja, o resultado será +infinito.
Lembre-se do teorema de limites infinitos, quando a constante do numerador for positiva (c>0) e o denominador tender a

, o resultado será +infinito. Se c<0 e o denominador tender a

, o resultado será -infinito, e por aí vai...
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Sáb Out 13, 2012 01:05
por MarceloFantini » Sáb Out 13, 2012 01:05
Atente para o fato de que sua notação está completamente errada. O correto é
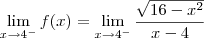
.
Semelhante para o segundo caso, onde você inclusive errou a notação da função: disse que era uma função da variável

quando na verdade é

. Troque uma das duas: escreva

ou

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Sáb Out 13, 2012 01:37
por Sobreira » Sáb Out 13, 2012 01:37
Obrigado pelas dicas.
E acabei não observando os detalhes das notações. Obrigado.
A questão da fatoração do denominador, eu fiquei confuso pois eu geralmente também resolvo de forma direta, mas em algumas resoluções de livros, eu vi autores utilizando a fatoração para a resolução do limite.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Sobreira » Seg Out 29, 2012 23:29
por Sobreira » Seg Out 29, 2012 23:29
Fala galera,
Estou neste tópico aki de novo pra comentar um fato que ocorreu a respeito dessa dúvida.
Hoje fiz uma prova de cálculo e antes da prova um colega questionou ao professor um exercício de limite infinito.
O professor disse que não aceitava a resolução por este método (aproximando dos valores para onde x estava tendendo) e só aceitaria caso todo denominador fosse racionalizado pois o procedimento de aproximação estava errado pois não era preciso e era impossível chegar a um valor tão próximo do valor para o qual x está convergindo.
(Não sei se fui bem claro).
Eu resolvi então fatorando o denominador....mas fiquei com essa dúvida agora novamente.Resolvi mais de 60 exercícios por aproximação e a resposta bateu exatamente como o gabarito.....já pesquisei em livros e os autores descrevem este procedimento como sendo válido....
E agora???
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Ter Out 30, 2012 07:13
por MarceloFantini » Ter Out 30, 2012 07:13
Sobreira, confesso que não entendi bem qual foi o problema. Você poderia citar um exemplo de um exercício que você fez, incluindo toda a explicação e procedimento, e dizer que parte exatamente seu professor disse que era inválido?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Ter Out 30, 2012 08:19
por Sobreira » Ter Out 30, 2012 08:19
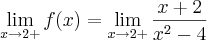
Tomando este exercício como exemplo:
O meu questionamento inicial era de que, substituindo o valor para o qual x está tendendo na questão (neste caso 2) de cara é possível verificar que teremos cte/0.

Bom, o que eu gostaria de saber, é se a partir deste instante eu poderia utilizar valores próximos de 2 pela direita (neste caso) para suspeitar o comportamento do infinito se (

ou

).
Resolvendo este:
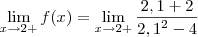
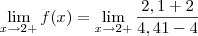
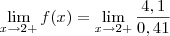
Este resultado nos levaria a suspeitar que se trata de um limite tendendo ao infinito positivo (

).
E então o professor informou que não aceitaria este procedimento, então por consequência, teríamos que fatorar o denominador para a resolução do exercício (minha dúvida inicial respondida pelo colega MrJuniorFerr neste mesmo tópico).
Como eu disse, resolvi vários exercícios desta forma e as respostas foram corretas e mesmo que com este procedimento, eu esteja "apenas" investigando o comportamento do infinito, gostaria de saber se é válido ou não este procedimento.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Ter Out 30, 2012 09:07
por MarceloFantini » Ter Out 30, 2012 09:07
Vamos tomar alguns cuidados.
Sobreira escreveu:O meu questionamento inicial era de que, substituindo o valor para o qual x está tendendo na questão (neste caso 2) de cara é possível verificar que teremos cte/0.

Bom, o que eu gostaria de saber, é se a partir deste instante eu poderia utilizar valores próximos de 2 pela direita (neste caso) para suspeitar o comportamento do infinito se (

ou

).
Resolvendo este:
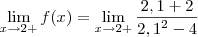
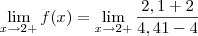
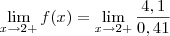
Este resultado nos levaria a suspeitar que se trata de um limite tendendo ao infinito positivo (

)
Primeiro, você está errando grosseiramente a notação ao fazer isto:

. Se você 'substituiu' o ponto, por definição não pode escrever o limite junto. Como comentário ao seu método, isto não é uma resolução, porém é válido que você faça tais investigações para entender o comportamento da função. Adotar isto como resposta, no entanto, é errado.
Sobreira escreveu:E então o professor informou que não aceitaria este procedimento, então por consequência, teríamos que fatorar o denominador para a resolução do exercício (minha dúvida inicial respondida pelo colega MrJuniorFerr neste mesmo tópico).
Como eu disse, resolvi vários exercícios desta forma e as respostas foram corretas e mesmo que com este procedimento, eu esteja "apenas" investigando o comportamento do infinito, gostaria de saber se é válido ou não este procedimento.
O seu professor está correto ao não aceitar este procedimento numa resolução, mas ele está errado quanto à "validade" disto, no sentido em que isso contribui, sim, para entender melhor o comportamento da função. No entanto, como já disse, você
não pode escrever isto numa resolução. Neste exemplo mesmo, a resolução deveria ser algo como:
Escrevendo
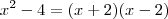
, teremos que o limite torna-se
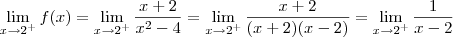
,
onde o denominador irá para zero pela direita, logo positivo, enquanto que o numerador permanece constante, portanto

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- limites infinitos
por oleve » Qua Jan 21, 2009 18:15
- 1 Respostas
- 3024 Exibições
- Última mensagem por Sandra Piedade

Sáb Jan 24, 2009 22:30
Cálculo: Limites, Derivadas e Integrais
-
- Limites Infinitos. Ajuda
por valeuleo » Qua Jun 22, 2011 12:39
- 4 Respostas
- 3133 Exibições
- Última mensagem por renatav

Dom Jun 26, 2011 22:46
Cálculo: Limites, Derivadas e Integrais
-
- Limites infinitos com modulo.
 por Sobreira » Sex Out 12, 2012 18:04
por Sobreira » Sex Out 12, 2012 18:04
- 13 Respostas
- 9038 Exibições
- Última mensagem por Sobreira

Sex Out 12, 2012 23:43
Cálculo: Limites, Derivadas e Integrais
-
- Limites infinitos com raiz
por Erick » Sáb Mar 30, 2013 11:11
- 1 Respostas
- 2894 Exibições
- Última mensagem por young_jedi

Sáb Mar 30, 2013 12:05
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limites infinitos envolvendo série
 por davifd_ » Ter Ago 18, 2015 15:56
por davifd_ » Ter Ago 18, 2015 15:56
- 10 Respostas
- 10646 Exibições
- Última mensagem por nakagumahissao

Qua Ago 19, 2015 09:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f (x) \lim_{4-}\frac{\sqrt[]{16-{x}^{2}}}{x-4} f (x) \lim_{4-}\frac{\sqrt[]{16-{x}^{2}}}{x-4}](/latexrender/pictures/ce6d42505c105a7702d299f740a0fa83.png)
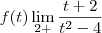


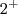 , substituindo 2,01 em t no denominador, você obtém um valor maior que zero, ou seja, o resultado será +infinito.
, substituindo 2,01 em t no denominador, você obtém um valor maior que zero, ou seja, o resultado será +infinito. , o resultado será +infinito. Se c<0 e o denominador tender a
, o resultado será +infinito. Se c<0 e o denominador tender a 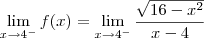 .
. quando na verdade é
quando na verdade é  . Troque uma das duas: escreva
. Troque uma das duas: escreva  ou
ou  .
.

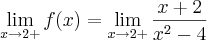

 ou
ou  ).
).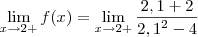
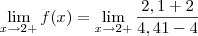
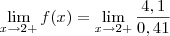
 ).
). . Se você 'substituiu' o ponto, por definição não pode escrever o limite junto. Como comentário ao seu método, isto não é uma resolução, porém é válido que você faça tais investigações para entender o comportamento da função. Adotar isto como resposta, no entanto, é errado.
. Se você 'substituiu' o ponto, por definição não pode escrever o limite junto. Como comentário ao seu método, isto não é uma resolução, porém é válido que você faça tais investigações para entender o comportamento da função. Adotar isto como resposta, no entanto, é errado.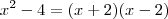 , teremos que o limite torna-se
, teremos que o limite torna-se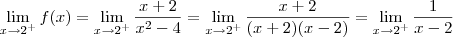 ,
, .
.

 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
