 é equivalente a
é equivalente a  e que o dobro do numerador menos o denominador é igual a 4 calcule o valor de a.b
e que o dobro do numerador menos o denominador é igual a 4 calcule o valor de a.b =
=
2.a-b=4
consegui montar mais não sei resolver me ajudem

 é equivalente a
é equivalente a  e que o dobro do numerador menos o denominador é igual a 4 calcule o valor de a.b
e que o dobro do numerador menos o denominador é igual a 4 calcule o valor de a.b =
=

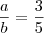 , então
, então  . Da segunda equação, se
. Da segunda equação, se 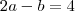 então
então 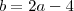 , logo
, logo 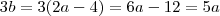 . Termine.
. Termine.

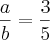

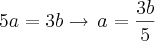
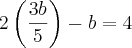



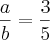
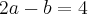

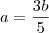
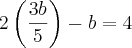
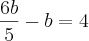
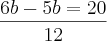
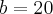
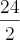





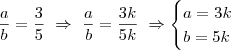
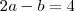
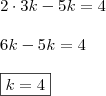
 e
e  substitua
substitua  por 4, isto é:
por 4, isto é: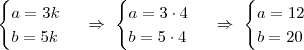
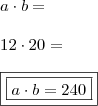


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

