Distância de frenagem é aquela percorrida por um carro do instante em que seu freio é acionado até o momento em que ele para. Essa distância é diretamente proporcional ao quadrado da velocidade que o carro está desenvolvendo no instante em que o freio é acionado.
O gráfico abaixo indica a distância de frenagem d, em metros, percorrida por um carro, em função de sua velocidade , em quilômetros por hora.
http://www.revista.vestibular.uerj.br/l ... o/Q4_6.PNG
Admita que o freio desse carro seja acionado quando ele alcançar a velocidade de 100 km/h. Calcule sua distância de frenagem, em metros.
Alguém poderia me explicar, o por que da constante k?
d = kv²
Por que foi usado esse k?
Tenho a resposta caso alguém queira.
Obrigado.


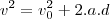
 é a velocidade incicial d é a distancia percorrida e a é a aceleração
é a velocidade incicial d é a distancia percorrida e a é a aceleração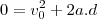

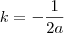
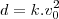



 .
.
 :
: