Escreva uma equação do plano que contém o ponto (1,-2,3) e é perpendicular a cada um dos planos
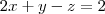e 
.Ao meu modo de ver, há duas soluções possíveis.
Uma delas é:
Os vetores normais
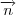dos planos: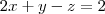 
=(2,1,-1) e 
=(1,-1,-1) são paralelos ao plano que contém o ponto (1,-2,3). Se eu fizer X , vou obter um vetor normal ao plano que no qual quero encontrar a equação? Acredito que seja uma solução, mas ainda tenho minhas dúvidas. Estou certo?O outro modo é:
Encontrar dois pontos pertencentes a um dos planos dados, por exemplo A(x,y,z) e B(x,y,z) e fazendo
e este vetor seria um vetor normal ao plano que quero encontrar sua equação.Mas aí vai a pergunta:
Como encontrar dois pontos de um plano?
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.