 por rafiusk » Dom Out 07, 2012 00:44
por rafiusk » Dom Out 07, 2012 00:44

essa integral no meu desenvolvimento deu

.
Já na resposta do professor deu a seguinte
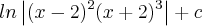
sei que ele simplifica ao máximo. Minha resposta simplificando não ficaria igual não né?
-
rafiusk
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Out 04, 2012 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por MrJuniorFerr » Dom Out 07, 2012 02:24
por MrJuniorFerr » Dom Out 07, 2012 02:24
rafiusk escreveu:
essa integral no meu desenvolvimento deu

.
Já na resposta do professor deu a seguinte
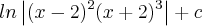
sei que ele simplifica ao máximo. Minha resposta simplificando não ficaria igual não né?

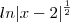
-
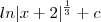
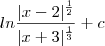
Não sei o que fazer após isto...
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Dom Out 07, 2012 03:39
por MarceloFantini » Dom Out 07, 2012 03:39
Quais foram as frações parciais que você encontrou? Poste estes cálculos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rafiusk » Dom Out 07, 2012 16:43
por rafiusk » Dom Out 07, 2012 16:43
MarceloFantini escreveu:Quais foram as frações parciais que você encontrou? Poste estes cálculos.

depois substitui por x=-2 e x =2 para zerar A e dps B.
Ficou assim
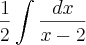
-

Que resultou naquele resultado do primeiro post.
-
rafiusk
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Out 04, 2012 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por MarceloFantini » Dom Out 07, 2012 20:14
por MarceloFantini » Dom Out 07, 2012 20:14
Por que você inverteu

e

? Quando for integrar isto torna-se

,
enquanto que você escreveu

e

, respectivamente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rafiusk » Seg Out 08, 2012 04:16
por rafiusk » Seg Out 08, 2012 04:16
Vlw Marcelo refiz aqui e deu tudo certo. Obrigado.
-
rafiusk
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Out 04, 2012 17:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- gabarito diferente da resposta
por jose henrique » Ter Out 12, 2010 01:10
- 2 Respostas
- 2128 Exibições
- Última mensagem por jose henrique

Seg Out 25, 2010 21:45
Funções
-
- resultado diferente da resposta
por natanskt » Seg Dez 06, 2010 13:39
- 1 Respostas
- 2187 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 14:01
Binômio de Newton
-
- Adição de Polinômios minha resposta diferente da do livro
por ravi » Ter Jan 31, 2012 14:02
- 2 Respostas
- 2253 Exibições
- Última mensagem por Arkanus Darondra

Ter Jan 31, 2012 14:49
Polinômios
-
- [cálculo] integração por frações simples
por procyon » Seg Nov 21, 2011 18:53
- 2 Respostas
- 1444 Exibições
- Última mensagem por LuizAquino

Seg Nov 21, 2011 20:57
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integração por frações Parciais
por MCG » Ter Abr 09, 2013 21:03
- 1 Respostas
- 1132 Exibições
- Última mensagem por young_jedi

Qua Abr 10, 2013 15:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 essa integral no meu desenvolvimento deu
essa integral no meu desenvolvimento deu  .
. 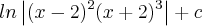 sei que ele simplifica ao máximo. Minha resposta simplificando não ficaria igual não né?
sei que ele simplifica ao máximo. Minha resposta simplificando não ficaria igual não né?
 essa integral no meu desenvolvimento deu
essa integral no meu desenvolvimento deu  .
. 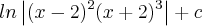 sei que ele simplifica ao máximo. Minha resposta simplificando não ficaria igual não né?
sei que ele simplifica ao máximo. Minha resposta simplificando não ficaria igual não né?
essa integral no meu desenvolvimento deu
.
sei que ele simplifica ao máximo. Minha resposta simplificando não ficaria igual não né?

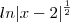 -
- 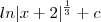
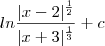



 depois substitui por x=-2 e x =2 para zerar A e dps B.
depois substitui por x=-2 e x =2 para zerar A e dps B.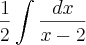 -
- 

 e
e  ? Quando for integrar isto torna-se
? Quando for integrar isto torna-se ,
, e
e  , respectivamente.
, respectivamente.


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.