Olá.
Estou com dificuldade em resolver um problema do volume 9 (Geometria Plana) da coleção 'Fundamentos da Matemática Elementar' DOLCE, O. POMPEU, J.N., para a determinação do raio do círculo, sendo que o triângulo retângulo possui catetos de medidas 6 e 8.
Tentei utilizar semelhança (de triângulos), mas não consegui associação entre lados de triângulo e diâmetro do círculo, neste caso.
Abraços.



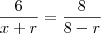
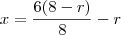



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)