Escreva uma equação do plano definido pelo ponto (2,1,3) e a interseção do plano
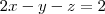 com um plano
com um plano  .
.Eu havia tentado fazer assim:
Sei que a equação de um plano
 é
é  , portanto, eu primeiramente deveria achar a interseção do plano
, portanto, eu primeiramente deveria achar a interseção do plano 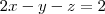 com o plano
com o plano  , que no caso será uma reta.
, que no caso será uma reta.Como z=0,

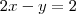
Isolando o y:

Isolando o x:
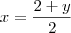
Ou seja, creio que o ponto de interseção destes dois planos seria:

O que fazer depois disto?


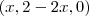
 e
e 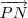
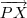 sera perpendicular ao vetor normal, ou seja o produto escalar entre eles é igual a 0
sera perpendicular ao vetor normal, ou seja o produto escalar entre eles é igual a 0

 , avisa que eu resolvo.
, avisa que eu resolvo.

