Dados:
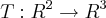 tal que T(1,1)=(3,2,1) e T(0,-2)=(0,1,0)
tal que T(1,1)=(3,2,1) e T(0,-2)=(0,1,0) tal que S(3,2,1)=(1,1), S(0,1,0)=(0,-2) e S(0,0,1)=(0,0)
tal que S(3,2,1)=(1,1), S(0,1,0)=(0,-2) e S(0,0,1)=(0,0)Ache a transformação linear
 tal que P=SoT.
tal que P=SoT.
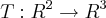 tal que T(1,1)=(3,2,1) e T(0,-2)=(0,1,0)
tal que T(1,1)=(3,2,1) e T(0,-2)=(0,1,0) tal que S(3,2,1)=(1,1), S(0,1,0)=(0,-2) e S(0,0,1)=(0,0)
tal que S(3,2,1)=(1,1), S(0,1,0)=(0,-2) e S(0,0,1)=(0,0) tal que P=SoT.
tal que P=SoT.



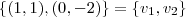 e
e 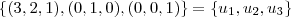 como bases de
como bases de  e
e  , respectivamente, então você tem que
, respectivamente, então você tem que 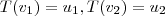 , enquanto que
, enquanto que  e
e 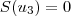 .
. e
e  , logo
, logo  é a aplicação identidade de
é a aplicação identidade de  .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: