Não entendi como resolver o exercício por favor me ajudem:
Calcule os valores de m e n para que seja exata a divisão do polinômio p(x) = 2x³ + mx² + nx - 1 por h(x) = 2x²- x - 1.



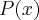 por um
por um 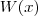 obtemos outro
obtemos outro  (o quociente e sobre um resto
(o quociente e sobre um resto 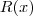 .
.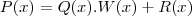 . Convenientemente, a divisão será dita EXATA se
. Convenientemente, a divisão será dita EXATA se 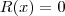 para todo
para todo  , isto é, o resto for identicamente nulo assim como na divisão de números inteiros.
, isto é, o resto for identicamente nulo assim como na divisão de números inteiros.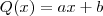 e o resto também o deve ser!
e o resto também o deve ser!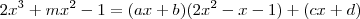
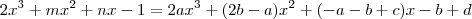
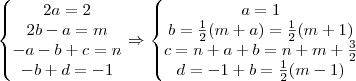
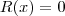 , então
, então 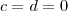 . Assim,
. Assim,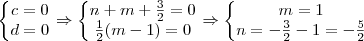


 por um de grau
por um de grau  o quociente será sempre de grau
o quociente será sempre de grau  . E eu acredito que o grau do resto será do mesmo grau que o quociente.
. E eu acredito que o grau do resto será do mesmo grau que o quociente.
Malorientado escreveu:Não entendi como resolver o exercício por favor me ajudem:
Calcule os valores de m e n para que seja exata a divisão do polinômio p(x) = 2x³ + mx² + nx - 1 por h(x) = 2x²- x - 1.
Russman escreveu:Quando dividimos um polinômiopor um
obtemos outro
(o quociente e sobre um resto
.
Ou seja,. Convenientemente, a divisão será dita EXATA se
para todo
, isto é, o resto for identicamente nulo assim como na divisão de números inteiros.
Como dividiremos um polinômio de 3° grau por um de 2° é possível mostrar que o quociente será do 1° grau. Assim,e o resto também o deve ser!
Logo
de onde, por igualdade de polinomios,
Como, então
. Assim,
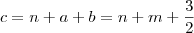 , o coreto seria
, o coreto seria 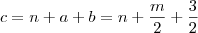 . Efetuando essa correção, obtemos que o resultado final será m = 1 e n = -2.
. Efetuando essa correção, obtemos que o resultado final será m = 1 e n = -2.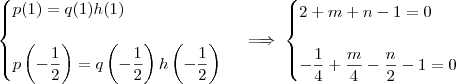
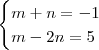
Russman escreveu:Se você dividir um polinômio de grau n por um de grau m o quociente será sempre de grau n-m. E eu acredito que o grau do resto será do mesmo grau que o quociente.
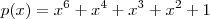 por
por 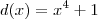 . Nesse caso, você perceberá que o grau do resto será maior do que o grau do quociente.
. Nesse caso, você perceberá que o grau do resto será maior do que o grau do quociente.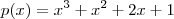 por
por 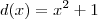 . Nesse caso, você perceberá que o grau do resto será igual ao grau do quociente.
. Nesse caso, você perceberá que o grau do resto será igual ao grau do quociente.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.



