Primeiramente gostaria de me apresentar, sou Marlon, sou novo por aqui e estou iniciando meus estudos para as específicas em engenharia mecânica, e como (quase) todo estudante do ensino médio tenho muitas dificuldades. Vamos a questão, depois ao que eu entendi, depois direi minha dúvida:
Admita dois números inteiros positivos, representados por a e b. Os restos das divisões de a e b por 8 são, respectivamente, 7 e 5.
Determine o resto da divisão do produto a.b por 8.
É o seguinte, as minhas conclusões (me corrijam caso eu esteja errado,por favor):
a pode ser infinitos números, mas existe uma maneira de representar, que é multiplicando o 8 por um número e somando ao resto da divisão. Chamei o este numero que multiplica de x.
a = 8.x + 7
A mesma coisa com b, chamando o número que multiplica o 8 de y:
b = 8.y + 5
Agora vamos ao produto:
a.b = (8x + 7).(8y + 5) = 64xy + 40x + 56y + 35
Aí está minha dúvida, não sei como prosseguir..
Tenho dúvidas em várias questões, meu ensino fundamental e médio foram bem abaixo da média, gostaria de contar com a ajuda de vocês.
Um abraço, obrigado!





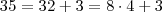 , daí usou a distributiva.
, daí usou a distributiva.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)