Verifique se os pontos dados a seguir são colineares, isto é, pertencem a uma mesma reta:
(a) A = (5,1,-3), B = (0,3,4) e C = (0,3,-5);
(b) A = (-1,1,3), B = (4,2,-3) e C = (14,4,-15);
Bom, se isso fosse no plano...beleza, eu pegava dois pontos e tentava encontrar a equação da reta...
Mas eu não tenho a menor idéia do que fazer quando estamos no espaço. Como resolver utilizando o conhecimento de vetores? Grato desde já ; )


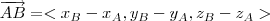 e
e 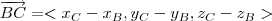 e compare-os.
e compare-os.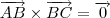 , isto é, existe algum
, isto é, existe algum  real tal que
real tal que 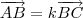
 ,
, e
e  pertencem a uma mesma reta. Do contrário, não.
pertencem a uma mesma reta. Do contrário, não.
 .
.



