 por Danilo » Qui Set 27, 2012 11:33
por Danilo » Qui Set 27, 2012 11:33
Verifique se os pontos dados a seguir são colineares, isto é, pertencem a uma mesma reta:
(a) A = (5,1,-3), B = (0,3,4) e C = (0,3,-5);
(b) A = (-1,1,3), B = (4,2,-3) e C = (14,4,-15);
Bom, se isso fosse no plano...beleza, eu pegava dois pontos e tentava encontrar a equação da reta...
Mas eu não tenho a menor idéia do que fazer quando estamos no espaço. Como resolver utilizando o conhecimento de vetores? Grato desde já ; )
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Qui Set 27, 2012 12:18
por young_jedi » Qui Set 27, 2012 12:18
Fazendo B-A, voce encontrara o vetor AB e fazendo C-A voce encontrara o vetor CA, se os pontos são colineares então os dois vetores tem a mesma direção, ou seja seu produto vetorial é igual a 0.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Russman » Qui Set 27, 2012 15:52
por Russman » Qui Set 27, 2012 15:52
É bem como o amigo ali falou.
Calcule os vetores
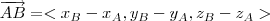
e
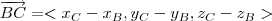
e compare-os.
Se
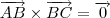
, isto é, existe algum

real tal que
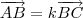
então os pontos

,

e

pertencem a uma mesma reta. Do contrário, não.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Danilo » Qui Set 27, 2012 20:35
por Danilo » Qui Set 27, 2012 20:35
Russman escreveu:É bem como o amigo ali falou.
Calcule os vetores
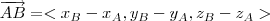
e
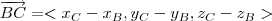
e compare-os.
Se
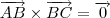
, isto é, existe algum

real tal que
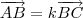
então os pontos

,

e

pertencem a uma mesma reta. Do contrário, não.
s
Então, tem como resolver sem utilizar o conhecimento de produto vetorial? Eu apenas vi ''vetores no plano e no espaço''. E que se há um vetor do tipo AB = cBC os dois vetores serão paralelos.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Qui Set 27, 2012 20:46
por young_jedi » Qui Set 27, 2012 20:46
Sim, voce tem que provar que AC igual k.AB, onde k é um numero real
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [VETORES]Alguém me ajuda com vetores?
por LAZAROTTI » Seg Set 17, 2012 00:49
- 2 Respostas
- 7373 Exibições
- Última mensagem por young_jedi

Seg Set 17, 2012 11:28
Geometria Analítica
-
- [Vetores] Módulo e Versor de vetores
por LAZAROTTI » Sáb Set 22, 2012 22:42
- 1 Respostas
- 2996 Exibições
- Última mensagem por young_jedi

Sáb Set 22, 2012 22:50
Geometria Analítica
-
- [Vetores] Produto Entre Vetores
por _bruno94 » Qua Jul 10, 2013 00:34
- 1 Respostas
- 5216 Exibições
- Última mensagem por temujin

Qua Jul 10, 2013 14:27
Geometria Analítica
-
- [Vetores] Vetores iguais
por KleinIll » Dom Nov 04, 2012 12:17
- 2 Respostas
- 3409 Exibições
- Última mensagem por KleinIll

Dom Nov 04, 2012 13:50
Geometria Analítica
-
- [Vetores] Operações com vetores
por IlgssonBraga » Qui Jul 18, 2013 11:42
- 1 Respostas
- 2387 Exibições
- Última mensagem por Russman

Qui Jul 18, 2013 15:45
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


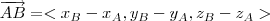 e
e 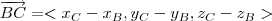 e compare-os.
e compare-os.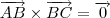 , isto é, existe algum
, isto é, existe algum  real tal que
real tal que 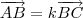
 ,
, e
e  pertencem a uma mesma reta. Do contrário, não.
pertencem a uma mesma reta. Do contrário, não. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
