 por GABRIELA » Qua Set 02, 2009 16:13
por GABRIELA » Qua Set 02, 2009 16:13
Se
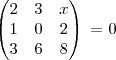
Então o valor de x é?
Fiz a questão usando a teoria de Sarrus, mas achei como resposta 3 e não é.
Acho que estou errando na hora de formar a equação mas não consigo ver o erro.

-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Qua Set 02, 2009 19:08
por Elcioschin » Qua Set 02, 2009 19:08
Gabriela
Você deve seguir as Regras do Fórum acima: Mostre as suas tentativas e o gabarito.
Se você não consegue "descobrir seu erro" lendo o seu próprio rascunho, como é que você quer que nós descubramos, sem ler o que você fez!
Além disso, este problema é totalmente básico: Você não está sabendo usar Sarrus, o que denota desconhecimento teórico do assunto.
Aconselho, portanto, que você estude primeiro a teoria para só depois tentar resolver problemas.
A solução é x = 5
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Molina » Qua Set 02, 2009 19:11
por Molina » Qua Set 02, 2009 19:11
GABRIELA escreveu:Se
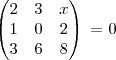
Então o valor de x é?
Fiz a questão usando a teoria de Sarrus, mas achei como resposta 3 e não é.
Acho que estou errando na hora de formar a equação mas não consigo ver o erro.

Boa noite, Gabriela.
Ficaria assim:
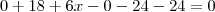
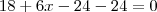
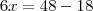
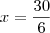

É isso?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por GABRIELA » Qui Set 03, 2009 19:12
por GABRIELA » Qui Set 03, 2009 19:12
Agora eu vi o errro.Por isso que erro muita questão por causa do sinal.
-24-24..Valeu!

-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda com uma questao de matriz e trigonometria
por Thiago Silveira » Qua Dez 22, 2010 19:58
- 1 Respostas
- 1591 Exibições
- Última mensagem por davi_11

Qui Dez 23, 2010 15:38
Matrizes e Determinantes
-
- Questão prova concurso - matriz
por fernandocez » Sáb Mar 26, 2011 10:21
- 3 Respostas
- 2104 Exibições
- Última mensagem por fernandocez

Sáb Mar 26, 2011 12:28
Matrizes e Determinantes
-
- duvida do exercicio de matriz
por pavaroti » Dom Nov 22, 2009 15:24
- 0 Respostas
- 835 Exibições
- Última mensagem por pavaroti

Dom Nov 22, 2009 15:24
Matrizes e Determinantes
-
- Matriz - Dúvida em Determinante
por noelsilva » Qui Ago 14, 2014 16:38
- 1 Respostas
- 6704 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 15, 2014 19:02
Matrizes e Determinantes
-
- duvida sobre inverso mod m de matriz
por gwirith » Dom Mai 17, 2009 21:11
- 0 Respostas
- 1961 Exibições
- Última mensagem por gwirith

Dom Mai 17, 2009 21:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
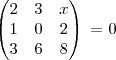


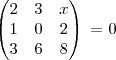



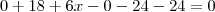
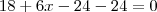
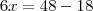
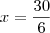





 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.