 por Bia_Oliveira » Ter Set 25, 2012 10:35
por Bia_Oliveira » Ter Set 25, 2012 10:35
Com relação à função quadrática f(x)+ -x²+2x-1, é fato que:
a) As suas raízes são iguais
b) O valor mínimo da função é positivo
c) O valor mínimo da função é negativo
d) A concavidade da parábola é positiva
e) As raízes são simétricas em relação ao eixo y.
-
Bia_Oliveira
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Set 20, 2012 10:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Ter Set 25, 2012 16:09
por young_jedi » Ter Set 25, 2012 16:09
encontre as raizes da equção
encontre o vertice da parabola
lembre-se que uma função do segundo grau, quando o sinal do coeficiente de

é positivo, a concavidade da parabola é voltada para cima e quando o sinal é negativo a concavidade é voltada para baixo.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Russman » Ter Set 25, 2012 21:43
por Russman » Ter Set 25, 2012 21:43
Com relação à função quadrática f(x)+ -x²+2x-1, é fato que:
a) As suas raízes são iguais
Calcule o discriminante da função. Se for positivo as raízes são reais e distintas. Se negativo, complexas conjugadas e se nulo iguais e reais.b) O valor mínimo da função é positivo
c) O valor mínimo da função é negativo
O valor extremo é dado por 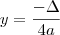 . Basta calculá-lo e observar o sinal.
. Basta calculá-lo e observar o sinal.d) A concavidade da parábola é positiva
Se o coeficiente do termo  for positivo então a concavidade é para cima. Se negativo, para baixo.
for positivo então a concavidade é para cima. Se negativo, para baixo.e) As raízes são simétricas em relação ao eixo y.
Somente se 
,
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bia_Oliveira » Qua Set 26, 2012 09:49
por Bia_Oliveira » Qua Set 26, 2012 09:49
Muito Obrigada!!
Consegui fazer o exercício, a resposta é a A.
-
Bia_Oliveira
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Set 20, 2012 10:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Qua Set 26, 2012 14:43
por Russman » Qua Set 26, 2012 14:43
Exato!

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bia_Oliveira » Dom Set 30, 2012 11:46
por Bia_Oliveira » Dom Set 30, 2012 11:46
Muito obrigada pela ajuda!!!

-
Bia_Oliveira
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Set 20, 2012 10:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercício prova SENAI
por Bia_Oliveira » Qua Set 26, 2012 10:34
- 1 Respostas
- 13111 Exibições
- Última mensagem por fraol

Sex Out 12, 2012 23:25
Álgebra Elementar
-
- Dúvida de P.A (Exercício prova SENAI)
por Bia_Oliveira » Qua Set 26, 2012 09:53
- 2 Respostas
- 2340 Exibições
- Última mensagem por Bia_Oliveira

Dom Set 30, 2012 11:45
Progressões
-
- SISTEMA DE EQUAÇÃO PROVA SENAI
por hatredshadows » Sex Nov 08, 2013 08:17
- 3 Respostas
- 3298 Exibições
- Última mensagem por e8group

Sex Nov 08, 2013 20:53
Sistemas de Equações
-
- Dúvida em exercício - função quadrática
por Danilo » Qua Jun 06, 2012 04:41
- 1 Respostas
- 1612 Exibições
- Última mensagem por e8group

Qua Jun 06, 2012 10:56
Funções
-
- [Dúvida exercício função quadrática]
por Aprendiz2012 » Dom Ago 19, 2012 12:54
- 4 Respostas
- 2676 Exibições
- Última mensagem por Aprendiz2012

Seg Ago 20, 2012 20:49
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 é positivo, a concavidade da parabola é voltada para cima e quando o sinal é negativo a concavidade é voltada para baixo.
é positivo, a concavidade da parabola é voltada para cima e quando o sinal é negativo a concavidade é voltada para baixo.
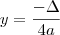 . Basta calculá-lo e observar o sinal.
. Basta calculá-lo e observar o sinal.

