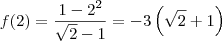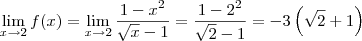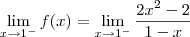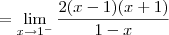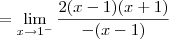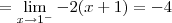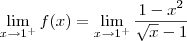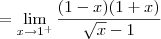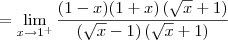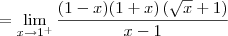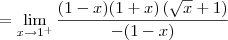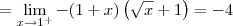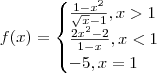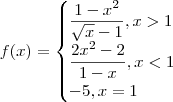por Cassiano » Ter Set 25, 2012 11:41
por Cassiano » Ter Set 25, 2012 11:41
Bom dia.
Tenho um problema matemático que estou com dificuldades para resolver.
Eu tenho um certo conhecimento dos conceitos básicos de limites e continuidade, mas estou tendo muitas dificuldades para resolver o problema abaixo, pois não consigo eliminar a indeterminação dos denominadores.
Verifique se a seguinte função é contínua nos pontos X:
![x = 0 , x = 2, f(x) =
\begin{align}
\frac{1-{x}^{2}}{\sqrt[]{x}-1} , x>1 \\
\frac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{align} x = 0 , x = 2, f(x) =
\begin{align}
\frac{1-{x}^{2}}{\sqrt[]{x}-1} , x>1 \\
\frac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{align}](/latexrender/pictures/085d26ff48c60cf914d82a78bf77aab8.png)
Não domino esta ferramenta de criação de equações, então talvez eu não tenha feito corretamente. Espero que entendam e possam me ajudar, pois preciso muito.
Eu não consegui inserir um colchete para agrupar as 3 funções.
Desde já agradeço.
Cassiano
Editado pela última vez por
Cassiano em Ter Set 25, 2012 14:27, em um total de 1 vez.
-
Cassiano
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Set 25, 2012 11:32
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por LuizAquino » Qua Set 26, 2012 08:17
por LuizAquino » Qua Set 26, 2012 08:17
Cassiano escreveu:Bom dia.
Tenho um problema matemático que estou com dificuldades para resolver.
Eu tenho um certo conhecimento dos conceitos básicos de limites e continuidade, mas estou tendo muitas dificuldades para resolver o problema abaixo, pois não consigo eliminar a indeterminação dos denominadores.
Verifique se a seguinte função é contínua nos pontos X:
![x = 0 , x = 2, f(x) =
\begin{align}
\frac{1-{x}^{2}}{\sqrt[]{x}-1} , x>1 \\
\frac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{align} x = 0 , x = 2, f(x) =
\begin{align}
\frac{1-{x}^{2}}{\sqrt[]{x}-1} , x>1 \\
\frac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{align}](/latexrender/pictures/085d26ff48c60cf914d82a78bf77aab8.png)
Você já sabe que uma função é contínua em x = 0 se acontecer

.
Analisando a função, note que:
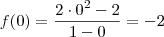
Já o limite será:
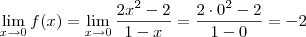
Conclusão: a função é contínua em x = 0.
De modo semelhante, a função é contínua em x = 2 se acontecer
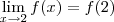
.
Analisando a função, note que:
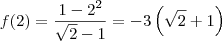
Já o limite será:
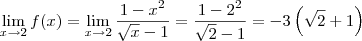
Conclusão: a função é contínua em x = 2.
Note que em nenhum dos dois casos houve uma indeterminação no cálculo do limite. Ou seja, em nenhum dos dois limites apareceu algo como "0/0". Portanto, não foi necessário efetuar simplificações.
Vamos imaginar agora que a pergunta fosse: essa função é contínua em x = 1?
Nesse caso, temos que f(1) = -5.
Já o limite lateral pela esquerda será:
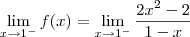
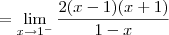
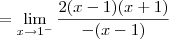
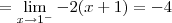
Só com esses dois resultados já podemos dizer que a função não é contínua em x = 1. Mas vamos calcular também o limite pela direita para treinar:
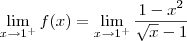
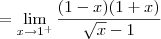
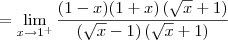
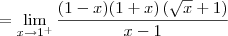
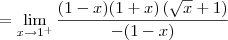
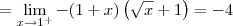
Cassiano escreveu:Não domino esta ferramenta de criação de equações, então talvez eu não tenha feito corretamente. Espero que entendam e possam me ajudar, pois preciso muito.
Eu não consegui inserir um colchete para agrupar as 3 funções.
Use o seguinte código:
- Código: Selecionar todos
[tex]
f(x) =
\begin{cases}
\frac{1-{x}^{2}}{\sqrt{x}-1} , x>1 \\
\frac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{cases}
[/tex]
O resultado desse código será:
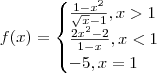
Para obter um resultado um pouco maior use o código:
- Código: Selecionar todos
[tex]
f(x) =
\begin{cases}
\dfrac{1-{x}^{2}}{\sqrt{x}-1} , x>1 \\
\dfrac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{cases}
[/tex]
O resultado desse código será:
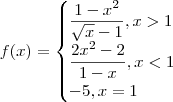
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Cassiano » Qua Set 26, 2012 09:04
por Cassiano » Qua Set 26, 2012 09:04
Muito obrigado pela ajuda.
Ainda bem que você se antecipou e resolveu para x=1, pois eu escrevi o enunciado errado. O Correto era de fato para x=1.
Muito obrigado mais uma vez.
Cassiano
-
Cassiano
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Set 25, 2012 11:32
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] indeterminação?
por rafaelbr91 » Ter Mar 27, 2012 18:48
- 3 Respostas
- 2225 Exibições
- Última mensagem por nietzsche

Ter Mar 27, 2012 19:31
Cálculo: Limites, Derivadas e Integrais
-
- Indeterminação de Limites
por dsidney30 » Sex Mai 03, 2013 15:53
- 1 Respostas
- 1547 Exibições
- Última mensagem por young_jedi

Dom Mai 05, 2013 19:07
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] - Indeterminação e Impossibilidade
por Scheu » Qui Fev 02, 2012 00:14
- 2 Respostas
- 3941 Exibições
- Última mensagem por Scheu

Sex Fev 03, 2012 00:03
Cálculo: Limites, Derivadas e Integrais
-
- Indeterminação limites fundamental
por Rosi7 » Sex Mai 22, 2015 11:49
- 3 Respostas
- 4742 Exibições
- Última mensagem por Jennicop

Ter Dez 22, 2015 03:20
Cálculo: Limites, Derivadas e Integrais
-
- Limites - Indeterminação do tipo 0X+infinito
por Pollyanna Moraes » Sáb Abr 28, 2012 15:04
- 1 Respostas
- 2948 Exibições
- Última mensagem por Guill

Dom Abr 29, 2012 09:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![x = 0 , x = 2, f(x) =
\begin{align}
\frac{1-{x}^{2}}{\sqrt[]{x}-1} , x>1 \\
\frac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{align} x = 0 , x = 2, f(x) =
\begin{align}
\frac{1-{x}^{2}}{\sqrt[]{x}-1} , x>1 \\
\frac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{align}](/latexrender/pictures/085d26ff48c60cf914d82a78bf77aab8.png)


 .
.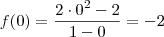
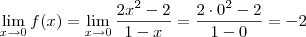
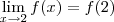 .
.