Cassiano escreveu:Bom dia.
Tenho um problema matemático que estou com dificuldades para resolver.
Eu tenho um certo conhecimento dos conceitos básicos de limites e continuidade, mas estou tendo muitas dificuldades para resolver o problema abaixo, pois não consigo eliminar a indeterminação dos denominadores.
Verifique se a seguinte função é contínua nos pontos X:
![x = 0 , x = 2, f(x) =
\begin{align}
\frac{1-{x}^{2}}{\sqrt[]{x}-1} , x>1 \\
\frac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{align} x = 0 , x = 2, f(x) =
\begin{align}
\frac{1-{x}^{2}}{\sqrt[]{x}-1} , x>1 \\
\frac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{align}](/latexrender/pictures/085d26ff48c60cf914d82a78bf77aab8.png)
Você já sabe que uma função é contínua em x = 0 se acontecer

.
Analisando a função, note que:
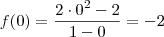
Já o limite será:
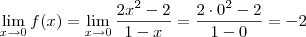
Conclusão: a função é contínua em x = 0.
De modo semelhante, a função é contínua em x = 2 se acontecer
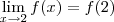
.
Analisando a função, note que:
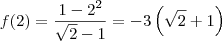
Já o limite será:
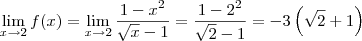
Conclusão: a função é contínua em x = 2.
Note que em nenhum dos dois casos houve uma indeterminação no cálculo do limite. Ou seja, em nenhum dos dois limites apareceu algo como "0/0". Portanto, não foi necessário efetuar simplificações.
Vamos imaginar agora que a pergunta fosse: essa função é contínua em x = 1?
Nesse caso, temos que f(1) = -5.
Já o limite lateral pela esquerda será:
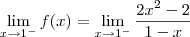
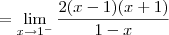
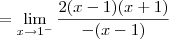
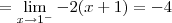
Só com esses dois resultados já podemos dizer que a função não é contínua em x = 1. Mas vamos calcular também o limite pela direita para treinar:
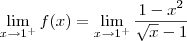
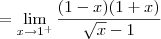
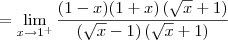
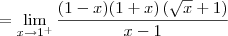
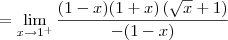
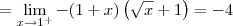
Cassiano escreveu:Não domino esta ferramenta de criação de equações, então talvez eu não tenha feito corretamente. Espero que entendam e possam me ajudar, pois preciso muito.
Eu não consegui inserir um colchete para agrupar as 3 funções.
Use o seguinte código:
- Código: Selecionar todos
[tex]
f(x) =
\begin{cases}
\frac{1-{x}^{2}}{\sqrt{x}-1} , x>1 \\
\frac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{cases}
[/tex]
O resultado desse código será:
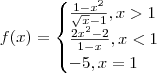
Para obter um resultado um pouco maior use o código:
- Código: Selecionar todos
[tex]
f(x) =
\begin{cases}
\dfrac{1-{x}^{2}}{\sqrt{x}-1} , x>1 \\
\dfrac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{cases}
[/tex]
O resultado desse código será:
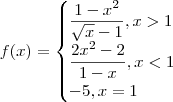
![x = 0 , x = 2, f(x) =
\begin{align}
\frac{1-{x}^{2}}{\sqrt[]{x}-1} , x>1 \\
\frac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{align} x = 0 , x = 2, f(x) =
\begin{align}
\frac{1-{x}^{2}}{\sqrt[]{x}-1} , x>1 \\
\frac{{2x}^{2}-2}{1-x}, x<1 \\
-5, x=1
\end{align}](/latexrender/pictures/085d26ff48c60cf914d82a78bf77aab8.png)


 .
.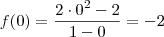
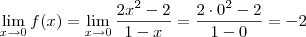
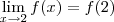 .
.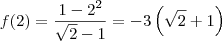
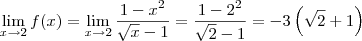
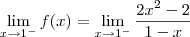
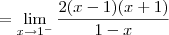
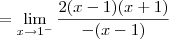
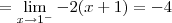
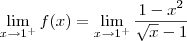
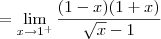
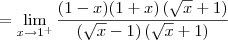
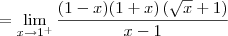
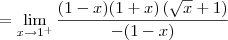
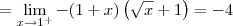
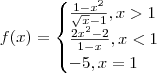
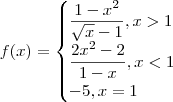


 .
.
 :
: