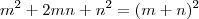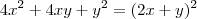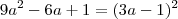por XxlucasxX » Ter Set 01, 2009 20:29
por XxlucasxX » Ter Set 01, 2009 20:29
Tem como explicar melhor Fatoração do trinômio quadrado perfeito.Expliquem detalhdo por favor.
-
XxlucasxX
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Set 01, 2009 20:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Ter Set 01, 2009 22:41
por Elcioschin » Ter Set 01, 2009 22:41
O que é um trinômio quadrado perfeito?
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Molina » Ter Set 01, 2009 23:21
por Molina » Ter Set 01, 2009 23:21
XxlucasxX escreveu:Tem como explicar melhor Fatoração do trinômio quadrado perfeito.Expliquem detalhdo por favor.
Boa noite, Lucas.
O Trinômio do quadrado perfeito só pode ser utilizado quando a expressão algébrica for um
trinômio (polinômio com três monômios) e esse trinômio formar um
quadrado perfeito.
Exemplos de trinômio: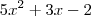
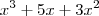
... etc.
Exemplo de quadrado perfeito:
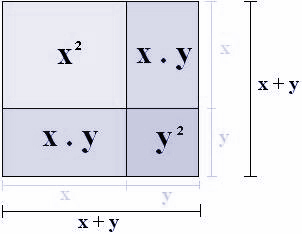
- trinomio.jpg (36.19 KiB) Exibido 2476 vezes
Esse quadrado foi dividido em quatro retângulos onde cada um tem a sua própria área, então a soma de todas essas áreas é a área total do quadrado maior, ficando assim:
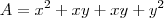
, como xy e xy são semelhantes podemos somá-los:
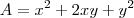
O resultado da área
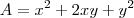
é um trinômio.
Outra fórmula para o cálculo da área do quadrado
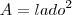
, então como o lado nesse quadrado é

, basta elevá-lo ao quadrado.
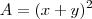
Logo, as área encontradas são iguais:
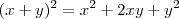 Note que em
Note que em 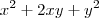 a raiz quadrada do primeiro termo, multiplicado pela raiz quadrada do terceiro termo, multiplicado por 2 é igual ao segundo termo.
a raiz quadrada do primeiro termo, multiplicado pela raiz quadrada do terceiro termo, multiplicado por 2 é igual ao segundo termo.Exemplos:
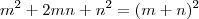
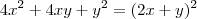
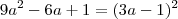
Coloco-me a disposição para maiores esclarecimentos.
Abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- PRECISO DE AJUDA !
por Layna Cardoso » Ter Mar 16, 2010 20:49
- 1 Respostas
- 2014 Exibições
- Última mensagem por Molina

Ter Mar 16, 2010 21:37
Problemas do Cotidiano
-
- PRECISO DE AJUDA!
por Lurdes » Sex Jul 09, 2010 23:22
- 1 Respostas
- 3419 Exibições
- Última mensagem por Neperiano

Qui Set 29, 2011 16:45
Problemas do Cotidiano
-
- preciso de ajuda...
por apoliveirarj » Qua Jul 21, 2010 12:25
- 5 Respostas
- 4175 Exibições
- Última mensagem por apoliveirarj

Qui Jul 22, 2010 12:52
Sistemas de Equações
-
- preciso de ajuda...
por apoliveirarj » Sáb Jul 24, 2010 19:10
- 1 Respostas
- 3049 Exibições
- Última mensagem por Neperiano

Sex Set 17, 2010 15:00
Estatística
-
- preciso de ajuda:
por angeloka » Ter Out 05, 2010 23:00
- 1 Respostas
- 2150 Exibições
- Última mensagem por MarceloFantini

Ter Out 05, 2010 23:39
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




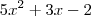
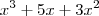
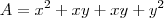 , como xy e xy são semelhantes podemos somá-los:
, como xy e xy são semelhantes podemos somá-los: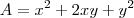
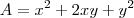 é um trinômio.
é um trinômio.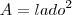 , então como o lado nesse quadrado é
, então como o lado nesse quadrado é  , basta elevá-lo ao quadrado.
, basta elevá-lo ao quadrado.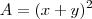
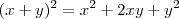
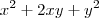 a raiz quadrada do primeiro termo, multiplicado pela raiz quadrada do terceiro termo, multiplicado por 2 é igual ao segundo termo.
a raiz quadrada do primeiro termo, multiplicado pela raiz quadrada do terceiro termo, multiplicado por 2 é igual ao segundo termo.