 por fabriel » Ter Set 25, 2012 02:57
por fabriel » Ter Set 25, 2012 02:57
Me ajudem nessa parte aqui que eu empaquei:
Então é dada essa função:
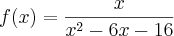
então derivei e deu isso:
![\frac{dy}{dx}=\frac{-x^2-16}{[x^2-6x-16]^2} \frac{dy}{dx}=\frac{-x^2-16}{[x^2-6x-16]^2}](/latexrender/pictures/c5e5526f5228d52b1fbe022b0a6a9bb0.png)
Ai agora é q entra a duvida. Estudando o sinal temos que o denominador vai ser sempre positivo né??, entretanto, no numerador, pareçe que não vai ter raiz real?? é isso.
Tem como alguém me mostrar o caminho por favor, obrigado.
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por LuizAquino » Ter Set 25, 2012 09:31
por LuizAquino » Ter Set 25, 2012 09:31
fabriel escreveu:Me ajudem nessa parte aqui que eu empaquei:
Então é dada essa função:
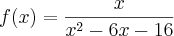
então derivei e deu isso:
![\frac{dy}{dx}=\frac{-x^2-16}{[x^2-6x-16]^2} \frac{dy}{dx}=\frac{-x^2-16}{[x^2-6x-16]^2}](/latexrender/pictures/c5e5526f5228d52b1fbe022b0a6a9bb0.png)
Ai agora é q entra a duvida. Estudando o sinal temos que o denominador vai ser sempre positivo né??, entretanto, no numerador, pareçe que não vai ter raiz real?? é isso.
Tem como alguém me mostrar o caminho por favor, obrigado.
O denominador é sempre positivo. Já o numerador é sempre negativo. Além disso, o numerador não tem raiz real. Desse modo, você irá concluir que f'(x) < 0 para todo x no domínio de f. Isso significa que o gráfico dessa função é sempre decrescente.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fabriel » Ter Set 25, 2012 12:57
por fabriel » Ter Set 25, 2012 12:57
Valeu obrigado.
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- crescimento e decrescimento
por joandro » Dom Abr 13, 2014 11:30
- 1 Respostas
- 1464 Exibições
- Última mensagem por alienante

Ter Abr 29, 2014 17:27
Cálculo: Limites, Derivadas e Integrais
-
- Intervalo de crescimento e decrescimento
por valeuleo » Qui Jun 23, 2011 12:02
- 4 Respostas
- 2839 Exibições
- Última mensagem por LuizAquino

Sáb Jun 25, 2011 16:50
Cálculo: Limites, Derivadas e Integrais
-
- crescimento e decrescimento da função
por Ana Maria da Silva » Qua Out 02, 2013 10:18
- 1 Respostas
- 1159 Exibições
- Última mensagem por Bravim

Qui Out 03, 2013 05:32
Cálculo: Limites, Derivadas e Integrais
-
- Intervalos de crescimento e decrescimento da função
por valeuleo » Ter Jun 21, 2011 21:50
- 3 Respostas
- 3439 Exibições
- Última mensagem por LuizAquino

Ter Jun 21, 2011 22:44
Cálculo: Limites, Derivadas e Integrais
-
- decrescimento,crescimento e pontos criticos
por LILI2016 » Ter Abr 19, 2016 09:57
- 0 Respostas
- 1349 Exibições
- Última mensagem por LILI2016

Ter Abr 19, 2016 09:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
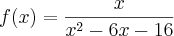
![\frac{dy}{dx}=\frac{-x^2-16}{[x^2-6x-16]^2} \frac{dy}{dx}=\frac{-x^2-16}{[x^2-6x-16]^2}](/latexrender/pictures/c5e5526f5228d52b1fbe022b0a6a9bb0.png)





 , avisa que eu resolvo.
, avisa que eu resolvo.

