Em um trajeto exclusivamente de subidas e descidas,um caminhante percorre 2 metros a cada segundo nas subidas e 3 metros a cada segundo nas descidas.
Se o caminhante percorreu, no trajeto todo, 1380 metros em 9 minutos e 40 segundos ,sem paradas, pode-se afirmar que, no total, ele:
resposta: subiu 60 metros a mais do que desceu.
Resolução.
Pensei em resolver igual exercícios de torneiras..
2 metros em 1/2 subida
3 metros em 1/3 descida
1/2-1/3= 1/6
Achei 1/6 ...
Bom 1.380metros em 9 minutos e 40 segundos .... travei....o que eu faço agora.
Ana Célia..


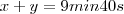

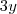
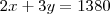

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)