[duvida] metodo de laguerre

por **ftdk** » Dom Set 23, 2012 10:17

Bom dia.

" Determine pelo metodo de Laguerre o intervalo que contenha todas as raizes reais da equacao ${x}^{5}-2{x}^{3}+{x}^{2}-2=0$ "

Exercicio relativamente simples, mas ao fazer a aproximacao da raiz, me deparei com nosso amigo zero. Minha duvida é se, nesse caso, eu devo coloca-lo em uma classificacao de positivo ou negativo apenas para terminar a resolucao, e lembrando que eu ainda nao conheço numeros complexos, mas o enunciado pediu apenas as raizes reais.

Até este momento, o resultado bate com o gabarito, pois o intervalo é ]-2;2[. Mas, se fosse necessário, como eu deveria proceder nessa situação ?

ps: tentei postar sem utilizar imagens externas, mas nao consegui inserir tabelas aqui. Existe algum tutorial para insercao de tabelas?

por **MarceloFantini** » Dom Set 23, 2012 13:34

Não entendo o que quer dizer exatamente, pois zero não é uma raíz deste polinômio. O que acontece é que o valor da função é negativo neste ponto. Marque apenas como raíz, não precisa classificá-lo como positivo ou negativo (mesmo porque ele é neutro).

Você poderia usar LaTeX para inserir a tabela.

por **ftdk** » Dom Set 23, 2012 15:05

Marcelo, obrigado pela resposta e desculpe se nao fui bem claro.

De acordo com o metodo de Laguerre, ao substituirmos os valores do intervalo ]-2;2[ na função, sempre que o resultado alternar entre + e -, significa que existe uma raiz real entre esses valores, correto? Por exemplo, existe 1 raiz real no intervalo ]1;2[

A minha duvida é quando substituo -1 na funcao. O resultado de f[-1] = 0, entao nao sei se em f[-1] eu considero positivo (acarretando em 1 raiz real entre ]-2;-1[, e 1 raiz real entre ]-1;0[ ) ou negativo (nao haveria nenhuma raiz real nesses intervalos).

por **MarceloFantini** » Dom Set 23, 2012 15:39

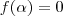Você está confundindo conceitos. A definição de raíz de uma função é justamente que $f( \alpha) =0$ . Quando você substitui -1 na função você vê que f(-1)=0

, logo -1 é raíz da função. Isto significa que qualquer intervalo contendo -1 fará com que a função assuma valores positivos e negativos.

por **ftdk** » Dom Set 23, 2012 18:24

Ah, então acho que tambem entendi porque não incluimos os extremos no intervalo ]-2;2[.

Agora, só por curiosidade, vou tentar calcular a menor e a maior raiz desse polinomio. Obrigado pela ajuda.