 por willwgo » Sáb Set 22, 2012 17:02
por willwgo » Sáb Set 22, 2012 17:02
se
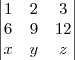
= -12 então
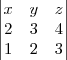
vale ?
preciso de ajuda nau consegui fazer ...
se conseguirem me expliquem como... desde já agradeço
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Sáb Set 22, 2012 17:20
por young_jedi » Sáb Set 22, 2012 17:20
se voce multiplica qualquer coluna ou linha de uma matriz A por um numero n, o determinante desta nova matriz será n vezes o determinante de A e se voce trocar duas linhas ou duas colunas de posição voce inverte o sinal do determinante.
repare que

ou seja a linha do meio esta multiplicada por 1/3
e repare tambem que a primeira linha foi trocada pela ultilma
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por willwgo » Sáb Set 22, 2012 17:40
por willwgo » Sáb Set 22, 2012 17:40
eu nau consegui entender ainda ... vc poderia resolver para eu poder entender melhor ...
é q eu to estudando sozinho e fiquei preso nesse exercicio
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por willwgo » Sáb Set 22, 2012 17:42
por willwgo » Sáb Set 22, 2012 17:42
ahhh acho q entendi a resposta vai ser - 4
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Sáb Set 22, 2012 22:23
por young_jedi » Sáb Set 22, 2012 22:23
o determinante da matriz

é -4 mais, mais o determinante da que voce quer encontrar, é o da matriz:

repare que de uma matriz para outra a diferença é que a primeira e a ultima linha estao trocadas,
como quando voce troca duas linhas ou duas colunas, voce inverte o sinal do determinate em o resultado sera 4.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- duvida do exercicio de matriz
por pavaroti » Dom Nov 22, 2009 15:24
- 0 Respostas
- 832 Exibições
- Última mensagem por pavaroti

Dom Nov 22, 2009 15:24
Matrizes e Determinantes
-
- Ufrgs
por Maria Livia » Seg Mar 18, 2013 19:18
- 3 Respostas
- 4800 Exibições
- Última mensagem por timoteo

Qua Mar 20, 2013 11:36
Geometria Plana
-
- ufrgs
por Maria Livia » Ter Set 03, 2013 12:41
- 1 Respostas
- 5554 Exibições
- Última mensagem por MateusL

Qua Set 04, 2013 11:20
Trigonometria
-
- Questões da UFRGS
por Neperiano » Qua Fev 11, 2009 18:32
- 3 Respostas
- 24240 Exibições
- Última mensagem por rcompany

Qui Fev 21, 2019 23:21
Desafios Enviados
-
- (UFRGS)Quadrilátero
por flavio2010 » Sex Jul 16, 2010 06:36
- 1 Respostas
- 2024 Exibições
- Última mensagem por Douglasm

Sex Jul 16, 2010 21:08
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
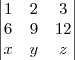 = -12 então
= -12 então 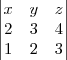 vale ?
vale ?
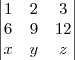 = -12 então
= -12 então 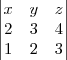 vale ?
vale ?








 .
.
 :
: