 por GABRIELA » Ter Set 01, 2009 14:15
por GABRIELA » Ter Set 01, 2009 14:15
Estou com a seguinte questão sobre matriz :
A =
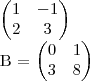
Então, calculando-se (a+b)², obtém-se quanto?
Então fiz ( a+b)² = (a+b).(a+b)
Meu resultado deu
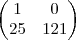
E no livro diz que a resposta é
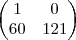
Onde estou errando ?
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Ter Set 01, 2009 14:21
por Molina » Ter Set 01, 2009 14:21
GABRIELA escreveu:Estou com a seguinte questão sobre matriz :
A =
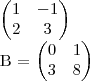
Então, calculando-se (a+b)², obtém-se quanto?
Então fiz ( a+b)² = (a+b).(a+b)
Meu resultado deu
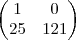
E no livro diz que a resposta é
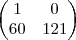
Onde estou errando ?
Boa tarde, Gabriela.
Você terá que fazer:
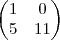
*
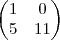
E este elemento que está dando diferente da resposta é dado por:
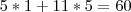
(igual ao gabarito do livro).
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por GABRIELA » Ter Set 01, 2009 14:47
por GABRIELA » Ter Set 01, 2009 14:47
molina escreveu:GABRIELA escreveu:Estou com a seguinte questão sobre matriz :
A =
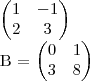
Então, calculando-se (a+b)², obtém-se quanto?
Então fiz ( a+b)² = (a+b).(a+b)
Meu resultado deu
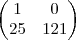
E no livro diz que a resposta é
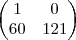
Onde estou errando ?
Boa tarde, Gabriela.
Você terá que fazer:
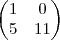
*
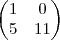
E este elemento que está dando diferente da resposta é dado por:
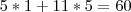
(igual ao gabarito do livro).
Bom estudo,

OK! Entendi como chegar no 60.Estava multiplicando de forma errada.Estva multiplicando coluna x coluna e na verdade é linha x coluna
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7158 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
-
- [Matriz]- inversa de uma matriz
por Ana_Rodrigues » Seg Mar 26, 2012 08:54
- 2 Respostas
- 3569 Exibições
- Última mensagem por Ana_Rodrigues

Seg Mar 26, 2012 18:05
Matrizes e Determinantes
-
- [MATRIZ]Determinante da Matriz 4x4
por LAZAROTTI » Qui Mai 03, 2012 22:33
- 1 Respostas
- 6724 Exibições
- Última mensagem por LuizAquino

Sex Mai 11, 2012 08:00
Matrizes e Determinantes
-
- [Matriz] Matriz com potencias
por rochadapesada » Dom Abr 07, 2013 20:29
- 3 Respostas
- 4697 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:32
Matrizes e Determinantes
-
- matriz
por Barbara » Ter Ago 18, 2009 15:26
- 4 Respostas
- 4806 Exibições
- Última mensagem por Molina

Qui Ago 20, 2009 18:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
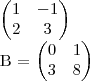
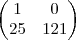
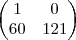

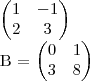
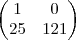
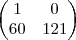

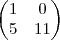 *
* 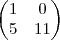
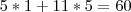 (igual ao gabarito do livro).
(igual ao gabarito do livro).

*
(igual ao gabarito do livro).

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)